Giải bài 87, 88, 89 trang 111, Bài 90 trang 112 Toán 8 tập 1: Ôn tập chương 1 hình học. Đáp án và hướng dẫn giải bài tập ôn tập chương 1 hình 8.
Danh sách bài học trong chương 1 Toán 8 tập 2 – Tứ Giác:
- Tứ giác
- Hình thang
- Hình thang cân
- Đường trung bình của tam giác, của hình thang
- Dựng hình bằng thước và compa. Dựng hình thang
- Đối xứng trục
- Hình bình hành
- Đối xứng tâm
- Hình chữ nhật
- Đường thẳng song song với một đường thẳng cho trước
- Hình thoi
- Hình vuông
- Ôn tập chương 1 hình học
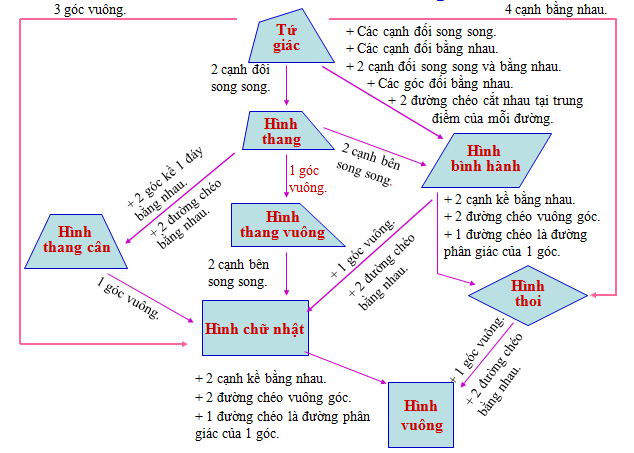Sơ đồ nhận biết các tứ giác – Ôn tập chương 1 hình 8 tập 1
Bài 87. Sơ đồ hình 109 biểu thị quan hệ giữa các tập hợp, hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống:
Tập hợp các hình chữ nhật là tập con của tập hợp các hình……………..
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình……………….
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình…………..
HD: Tập hợp các hình chữ nhật là tập con của tập hợp các hình thang, hình bình hành
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông
Bài 88 trang 111. Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì tứ giác EFGH là:
a) Hình chữ nhật ?
b) Hình thoi ?
c) Hình vuông ?
Đáp án bài 88:
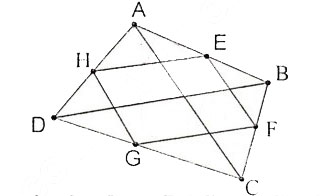
Ta có: HE, GF lần lượt là đường trung bình của ΔADB và Δ CDB
⇒ HE//BD, GF//BD và HE = GF = BD/2
Tương tự: HG, EF lần lượt là đường trung bình của ΔDAC và ΔBAC
⇒ HG//AC, EF //AC và HG = EF = AC/2
⇒ Tứ giác EFGH là hình bình hành.
a) Để hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF ⇒ BD ⊥ AC
Điều kiện phải tìm là: Hai đường chéo AC và BD vuông góc với nhau.
Advertisements (Quảng cáo)
b) Để hình bình hành EFGH là hình thoi thì EH = EF ⇒ BD = AC
Điều kiện phải tìm là: Hai đường chéo AC và BD bằng nhau
c) Để hình bình hành EFGH là hình vuông thì EFGH vừa là hình chữ nhật, vừa hình thoi. Suy ra BD ⊥ AC và BD = AC
Điều kiện phải tìm là: Hai đường chéo AC và BD vuông góc với nhau và bằng nhau.
Bài 89 trang 111 Ôn tập chương 1 hình học toán 8. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với điểm M qua AB.
a) Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c) Cho BC = 4 cm, tính chu vi tứ giác AEBM.
d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?
Advertisements (Quảng cáo)
a) Ta có: MB = MC (giả thiết)
DA = DB (Giả thiết)
⇒ DM là đường trung bình của Δ ABC
⇒ DM//AC
Mặt khác ABC vuông tại A
⇒ AC ⊥ AB ⇒ DM ⊥ AB ⇒ DE ⊥ AB (*)
E là điểm đối xứng với M qua D ⇒ DM = DE (**)
Từ (*) và (**) ta suy ra: Điểm E đối xứng với M qua AB
b) Ta có AB ⊥ EM và DE = DM, DA = DB
⇒ Tứ giác AEBM là hình thoi
⇒ AE//BM mà BM = MC ⇒ AE//MC và AE = MC
⇒ tứ giác AEMC là hình bình hàng
c) Ta có BC = 4 (cm) ⇒ BM = BC/2 = 2(cm)
Chu vi hình thoi ABEM là P = 4BM = 8 (cm)
d) Hình thoi AEBM là hình vuông khi góc ∠AMB = 900
⇒ AM ⊥ BC
Mặt khác: AM là trung tuyến của tam giác vuông ABC
Suy ra: Δ ABC vuông cân tại A
Điều kiện: Δ ABC vuông cân tại A
Bài 90.
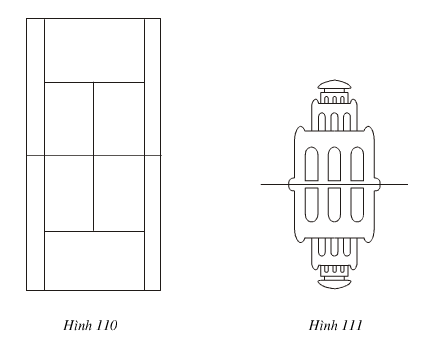Đố: Tìm trục đối xứng và tâm đối xứng của
a) Hình 110 (Sơ đồ một sân quần vợt)
b) Hình 111
a) Hình 110 (Sơ đồ một sân quần vợt): Có 2 trục đối xứng và 1 tâm đối xứng
b) Hình 111 Có 2 trục đối xứng và 1 tâm đối xứng.
Sau bài này các em sẽ có bài kiểm tra 1 tiết hình học. Chúc các em làm bài kiểm tra đạt kết quả tốt nhất.
Dethikiemtra.com
