Thi kì 1 môn Toán lớp 8: Hình vuông có độ dài đường chéo là 6cm. Độ dài cạnh hình vuông đó là bao nhiêu?

Hình vuông có độ dài đường chéo là \(6cm\). Độ dài cạnh hình vuông đó là bao nhiêu?; Kết quả của phép cộng: \(\dfrac{{3x – 1}}{{3x – 3}} + \dfrac{{ – 2}}{{3x – 3}}\)là? … trong đề Thi kì 1 môn Toán lớp 8:

Bài 1 (2đ)Chọn chữ cái trước đáp án đúng:

1.      Đa thức \(12x – 36 – {x^2}\) bằng:

A.    \( – {\left( {x + 6} \right)^2}\)

B.     \({\left( { – x – 6} \right)^2}\)

C.    \({\left( { – x + 6} \right)^2}\)

D.    \( – {\left( {x – 6} \right)^2}\)

2.      Kết quả của phép cộng: \(\dfrac{{3x – 1}}{{3x – 3}} + \dfrac{{ – 2}}{{3x – 3}}\)là:

A.    \(\dfrac{{3x + 1}}{{3x – 3}}\)

B.     \(\dfrac{{x + 1}}{{x – 3}}\)

C.    \(1\)

D.    \(\dfrac{{3x – 5}}{{3\left( {3x – 3} \right)}}\)

3.      Kết quả rút gọn biểu thức:\(\left( {x – 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) – \left( {x + 2y} \right)\left( {{x^2} – 2xy + 4{y^2}} \right)\) là:

A.    \( – 16{y^3}\)

B.     \( – 4{y^3}\)

C.    \(16{y^3}\)

D.    \( – 12{y^3}\)

4.      Số dư khi chia đa thức: \(3{x^4} – 2{x^3} + {x^2} – 2x + 2\) cho đa thức \(x – 2\) là:

A.    \(50\)

B.     \(34\)

C.    \(32\)

D.    \(30\)

5.      Hình vuông có độ dài đường chéo là \(6cm\). Độ dài cạnh hình vuông đó là:

A.    \(\sqrt {18} \,cm\)

B.     \(18\,cm\)

C.    \(3\,cm\)

D.    \(4\,cm\)

6.      Một hình chữ nhật có diện tích \(15{m^2}\). Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:

A.    \(30\,{m^2}\)

B.     \(45\,{m^2}\)

C.    \(90\,{m^2}\)

D.    \(75\,{m^2}\)

7.      Cho hình thang cân \(ABC{\rm{D}}\,\left( {AB//C{\rm{D}}} \right)\) có \(\angle A = {135^0}\) thì \(\angle C\) bằng:

A.    \({35^0}\)

B.     \({45^0}\)

C.    \({55^0}\)

D.    Không tính được.

8.      Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo bằng nhau là:

A.    Hình thang cân

B.     Hình chữ nhật

C.    Hình thoi

D.    Hình vuông

Bài 2 (1,0đ)Phân tích đa thức sau thành nhân tử:

a)\(6xy + 12x – 4y – 8\)

b)\({x^3} + 2{x^2} – x – 2\)

Bài 3 (1,5đ)

a)Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biểu thức: \({\left( {x – 2} \right)^2} – \left( {x – 1} \right)\left( {x + 1} \right) + 4\left( {x + 2} \right)\)

b)Tìm \(x\) biết: \(\left( {2 – x} \right)\left( {2 + x} \right) = 3\)

Bài 4 Thực hiện phép tính:

a)\(\dfrac{{x + 2}}{{x – 3}} – \dfrac{{{x^2} + 6}}{{{x^2} – 3x}}\)

b)\(\dfrac{{4x – 4}}{{{x^2} – 4x + 4}}:\dfrac{{{x^2} – 1}}{{{{\left( {2 – x} \right)}^2}}}\)

Bài 5 Cho \(\Delta ABC\) có \(A{\rm{D}}\) là phân giác của \(\angle BAC\;\,\,\left( {D \in BC} \right)\). Từ\(D\) kẻ các đường thẳng song song với \(AB\)  và \(AC\), chúng cắt \(AC,\,AB\) tại \(E\)  và \(F\).

a)Chứng minh: Tứ giác \(A{\rm{ED}}F\) là hình thoi.

b)Trên tia \(AB\) lấy điểm \(G\)  sao cho \(F\) là trung điểm \(AG\). Chứng minh: Tứ giác \(EFG{\rm{D}}\) là hình bình hành.

c)Gọi \(I\) là điểm đối xứng của \(D\)  qua \(F\) , tia \(IA\) cắt tia \(DE\) tại \(K\). Gọi \(O\) là giao điểm của \(A{\rm{D}}\)  và \(EF\). Chứng minh: \(G\) đối xứng với \(K\)  qua \(O\).

d)Tìm điều kiện của \(\Delta ABC\)để tứ giác \(A{\rm{D}}GI\) là hình vuông.

Bài 6 : Tính giá trị của biểu thức:\(\left( {1 – \dfrac{1}{{{2^2}}}} \right)\left( {1 – \dfrac{1}{{{3^2}}}} \right)\left( {1 – \dfrac{1}{{{4^2}}}} \right)…\left( {1 – \dfrac{1}{{{{2017}^2}}}} \right)\)

---

Bài 1.

1D	2C	3A	4B
5A	6C	7B	8C

Bài 2: \(\begin{array}{l}a)\,\,6xy + 12x – 4y – 8 = 6x\left( {y + 2} \right) – 4\left( {y + 2} \right)\\ = \left( {y + 2} \right)\left( {6x – 4} \right).\\b)\,\,{x^3} + 2{x^2} – x – 2 = {x^2}\left( {x + 2} \right) – \left( {x + 2} \right)\\ = \left( {x + 2} \right)\left( {{x^2} – 1} \right) = \left( {x + 2} \right)\left( {x + 1} \right)\left( {x – 1} \right).\end{array}\)

Bài 3: \(a)\,\,{\left( {x – 2} \right)^2} – \left( {x – 1} \right)\left( {x + 1} \right) + 4\left( {x + 2} \right)\)\(\; = {x^2} – 4x + 4 – {x^2} + 1 + 4x + 8 = 13\)

Do đó giá trị của biểu thức không phụ thuộc vào giá trị của biến.

\(\begin{array}{l}b)\,\,\left( {2 – x} \right)\left( {2 + x} \right) = 3\\ \Leftrightarrow 4 – {x^2} – 3 = 0\\ \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  – 1\end{array} \right..\end{array}\)

Bài 4: \(\begin{array}{l}a)\,\,\dfrac{{x + 2}}{{x – 3}} – \dfrac{{{x^2} + 6}}{{{x^2} – 3x}} = \dfrac{{\left( {x + 2} \right)x – {x^2} – 6}}{{x\left( {x – 3} \right)}}\;\;\;\;\left( {x \ne 0,\;\;x \ne 3} \right)\\\; = \dfrac{{{x^2} + 2x – {x^2} – 6}}{{x\left( {x – 3} \right)}} = \dfrac{{2\left( {x – 3} \right)}}{{x\left( {x – 3} \right)}} = \dfrac{2}{x}\\b)\,\,\dfrac{{4x – 4}}{{{x^2} – 4x + 4}}:\dfrac{{{x^2} – 1}}{{{{\left( {2 – x} \right)}^2}}}\;\;\;\;\left( {x \ne 2;\;x \ne  \pm 1} \right)\\\;\; = \dfrac{{4\left( {x – 1} \right)}}{{{{\left( {x – 2} \right)}^2}}}.\dfrac{{{{\left( {2 – x} \right)}^2}}}{{\left( {x – 1} \right)\left( {x + 1} \right)}} = \dfrac{4}{{x + 1}}.\end{array}\)

Bài 5.
 

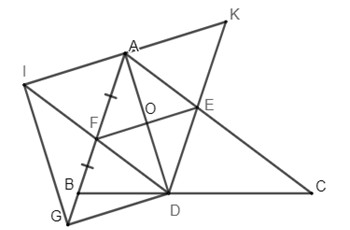
a)Xét tứ giác \(AFDE\) có: \(\left\{ \begin{array}{l}A{\rm{E}}//AF\\DF//A{\rm{E}}\end{array} \right.\left( {gt} \right) \Rightarrow AFDE\) là hình bình hành (dhnb)

Lại có, \(A{\rm{D}}\) là phân giác của \(\angle BAC\;\left( {gt} \right) \Rightarrow \) hình bình hành \(AFDE\) là hình thoi (dhnb)

b)Vì \(AFDE\) là hình thoi (cmt)

\( \Rightarrow E{\rm{D}} = AF\) (tính chất hình thoi)

Mà \(F\)  là trung điểm của \(AG\left( {gt} \right) \Rightarrow AF = FG\) (tính chất trungđ) \( \Rightarrow E{\rm{D}} = GF\left( { = AF} \right).\)

Mà \(GF//E{\rm{D}}\left( {gt} \right) \Rightarrow FEDG\) là hình hình hành (dhnb)

c)Vì \(I\)  là điểm đối xứng của \(D\)  qua \(F\)(gt) \( \Rightarrow F\) là trung điểm của \(I{\rm{D}}\) (tính chất hai điểm đối xứng qua mộtđ)

Xét tứ giác \(AIG{\rm{D}}\) có \(AG\) và \(DI\) cắt nhau tại trung điểm \(F\) của mỗi đường (cmt)

\( \Rightarrow AIG{\rm{D}}\) là hình bình hành (dhnb)

\( \Rightarrow AI//G{\rm{D}}\) (tính chất)

\( \Rightarrow G{\rm{D}}//AK\) (do \(I,\,A,\,K\) thẳng hàng) (1)

Lại có, \(DE//AB\left( {gt} \right) \Rightarrow DK//AG\) (2)

Từ (1) và (2) \( \Rightarrow AK{\rm{D}}G\) là hình bình hành (dhnb)

Mà hai đường chéo \(A{\rm{D}},\,GK\)cắt nhau tại trung điểm O nên suy ra \(G\) đối xứng với \(K\) qua \(O\). (đpcm)

d)Hình thoi \(IA{\rm{D}}G\) là hình vuông khi và chỉ \(\angle IA{\rm{D}} = {90^0} \Leftrightarrow \Delta ABC\) vuông tại \(A\).

Thật vậy, ta có: \(IA{\rm{D}}G\) là hình vuông nên suy ra \(\angle BA{\rm{D}} = {45^0}\)

  mà AD là phân giác của \(\angle BAC\left( {gt} \right) \Rightarrow \angle BAC = 2\angle BA{\rm{D}} = {2.45^0} = {90^0} \Rightarrow \Delta ABC\) vuông tại A.

Bài 6: \(\begin{array}{l}\;\;\;\left( {1 – \dfrac{1}{{{2^2}}}} \right)\left( {1 – \dfrac{1}{{{3^2}}}} \right)\left( {1 – \dfrac{1}{{{4^2}}}} \right)…\left( {1 – \dfrac{1}{{{{2017}^2}}}} \right)\\ = \dfrac{{\left( {{2^2} – 1} \right)\left( {{3^2} – 1} \right)\left( {{4^2} – 1} \right)…\left( {{{2017}^2} – 1} \right)}}{{{2^2}{{.3}^2}{{.4}^2}{{…2017}^2}}}\\ = \dfrac{{\left( {2 – 1} \right)\left( {2 + 1} \right)\left( {3 – 1} \right)\left( {3 + 1} \right)….\left( {2017 – 1} \right)\left( {2017 + 1} \right)}}{{{2^2}{{.3}^2}{{.4}^2}{{…2017}^2}}}\\ = \dfrac{{1.3.2.4…2016.2018}}{{{{\left( {2.3.4…2017} \right)}^2}}} = \dfrac{{1.2.{{\left( {3.4…2016} \right)}^2}.2017.2018}}{{{{\left( {1.2.3…2017} \right)}^2}}}\\ = \dfrac{{1.2.2017.2018}}{{{2^2}{{.2017}^2}}} = \dfrac{{2018}}{{2.2017}} = \dfrac{{1009}}{{2017}}.\end{array}\)