
Phần I: Trắc nghiệm khách quan (2,0đ)
Học sinh ghi đáp án đúng là A, B, C hoặc D vào tờ giấy thi
1 .Điều kiện xác định của biểu thức\(\sqrt {6 – 3x} \) là:
A.\(x \le 2\) B. \(x \ge 2\)
C. \(x \ge 0\) D.\(x < 2\)
2 .Giá trị nhỏ nhất của biểu thức \(p = \sqrt {x + 3} – 1\) là:
A.\(3\) B.\( – 1\)
C. \( – 3\) D.\(0\)
3 .Giá trị biểu thức \(P = \dfrac{{\sqrt x – 3}}{{\sqrt x + 3}}\)khi \(x = 4 – 2\sqrt 3 \) là:
A. \( – 11 + 6\sqrt 3 \) B. \(\dfrac{{ – 11 – 6\sqrt 3 }}{{13}}\)
C. \(\dfrac{{ – 5 – 12\sqrt 3 }}{{37}}\) D.\(1\)
4 .Cho tam giác ABC vuông tại A. Biết rằng \(\dfrac{{AB}}{{AC}} = \sqrt 3 \). Số đo độ của góc ABC bằng:
A. \({30^0}\) B. \({60^0}\)
C. \({45^0}\) D.\({50^0}\)
5 .Với giá trị nào của a thì hàm số \(y = \left( {a – 5} \right)x + 1\) đồng biến trên tập\(\mathbb{R}\)?
A. \(a < 5\) B. \(a > 5\)
C. \(a = 5\) D.\(a > – 5\)
6 .Cho hai đường thẳng\(\left( {{d_1}} \right)\)\(:\,\,y = 2x + 3\) và\(\left( {{d_2}} \right)\)\(:\,\,y = \left( {{m^2} + 1} \right)x + m + 2\) (với m là tham số). Với giá trị nào của tham số m thì đường thẳng \(\left( {{d_1}} \right)\) song song với đường thẳng \(\left( {{d_2}} \right)\)?
A. \(m = 2\)
B. \(m = 1\) hoặc\(m = – 1\)
C. \(m = 1\)
D.\(m = – 1\)
7 .Cho EM, EN là hai tiếp tuyến của đường tròn \(\left( O \right)\) với tiếp điểm M, N. Khẳng định nào sau đây là sai:
A. \(\angle EMO = {90^o}\)
B.Bốn điểm E, M, O, N cùng thuộc một đườngtròn
C. MN là trung trực của EO
D.OE là phân giác của\(\angle MON\)
8 .Hai đường tròn \(\left( {O;5} \right)\)và \(\left( {O’;8} \right)\) có vị trí tương đối với nhau như thế nào biết \(OO’ = 12\)
A. Tiếp xúc nhau
B. Không giao nhau
C. Tiếp xúc ngoài
D.Cắt nhau
Phần II: Tự luận (8,0đ)
Advertisements (Quảng cáo)
1. (2,0đ):Cho hai biểu thức \(A = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x }}{{\sqrt x – 3}} – \dfrac{{3x + 3}}{{x – 9}}\)và \(B = \dfrac{{\sqrt x + 1}}{{\sqrt x – 3}}\) với \(x \ge 0\,,\,\,x \ne 9\)
1) Rút gọn biểu thức A.
2) Tìm tất cả các giá trị của x để \(\dfrac{A}{B} < – \dfrac{1}{2}\).
2. (2,5đ):Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right)\)\(:\,\,y = ax + 3\).
1) Xác định a biết \(\left( d \right)\) đi qua \(K\left( {1; – 1} \right)\). Vẽ đồ thị với a vừa tìm được.
2) Tìm tất cả các giá trị của a để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.
3. (3,0đ):Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếpđ).
1) Chứng minh các điểm M, E, O, F cùng thuộc một đường tròn.
2) Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác MEF.
3) Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Chứng minh P là trung điểm của FK.
4. (0,5đ):Giải phương trình \({x^2} + x – 17 = \sqrt {\left( {{x^2} – 15} \right)\left( {x – 3} \right)} + \sqrt {{x^2} – 15} + \sqrt {x – 3} \)

Phần I: Trắc nghiệm khách quan
|
1A |
2B |
3A |
4A |
|
5B |
6D |
7C |
8D |
Phần II: Tự luận
1. Cho hai biểu thức \(A = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x }}{{\sqrt x – 3}} – \dfrac{{3x + 3}}{{x – 9}}\) và \(B = \dfrac{{\sqrt x + 1}}{{\sqrt x – 3}}\) với \(x \ge 0\,,\,\,x \ne 9\)
1) Rút gọn biểu thức A.
\(\begin{array}{l}A = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x }}{{\sqrt x – 3}} – \dfrac{{3x + 3}}{{x – 9}}\\ = \dfrac{{2\sqrt x .\left( {\sqrt x – 3} \right) + \sqrt x .\left( {\sqrt x + 3} \right) – \left( {3x + 3} \right)}}{{x – 9}}\\= \dfrac{{2x – 6\sqrt x + x + 3\sqrt x – 3x – 3}}{{x – 9}} \\= \dfrac{{ – 3\sqrt x – 3}}{{x – 9}}.\end{array}\)
2) Tìm tất cả các giá trị của x để \(\dfrac{A}{B} < – \dfrac{1}{2}\).
\(\begin{array}{l}\dfrac{A}{B} = \dfrac{{ – 3\sqrt x – 3}}{{x – 9}}:\dfrac{{\sqrt x + 1}}{{\sqrt x – 3}} \\\;\;\;= \dfrac{{ – 3\sqrt x – 3}}{{x – 9}}.\dfrac{{\sqrt x – 3}}{{\sqrt x + 1}} \\\;\;\;= \dfrac{{ – 3\left( {\sqrt x + 1} \right)\left( {\sqrt x – 3} \right)}}{{\left( {\sqrt x – 3} \right)\left( {\sqrt x + 3} \right)\left( {\sqrt x + 1} \right)}} \\\;\;\;= \dfrac{{ – 3}}{{\sqrt x + 3}}\\\dfrac{A}{B} < – \dfrac{1}{2} \Leftrightarrow \dfrac{{ – 3}}{{\sqrt x + 3}} < – \dfrac{1}{2} \\\Leftrightarrow \dfrac{3}{{\sqrt x + 3}} > \dfrac{1}{2}\\ \Leftrightarrow 6 > \sqrt x + 3 \Leftrightarrow \sqrt x < 3 \Leftrightarrow x < 9.\end{array}\)
Kết hợp điều kiện đầu bài \( \Rightarrow \)\(0 \le x < 9.\)
Vậy với mọi \(0 \le x < 9\) thỏa mãn yêu cầu đề bài.
2. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right)\)\(:\,\,y = ax + 3\).
Advertisements (Quảng cáo)
1) Xác định a biết \(\left( d \right)\) đi qua \(K\left( {1; – 1} \right)\). Vẽ đồ thị với a vừa tìm được.
\(\left( d \right)\) đi qua \(K\left( {1; – 1} \right)\)\( \Rightarrow – 1 = a.1 + 3 \Leftrightarrow a = – 4\)
Vậy với \(a = – 4\) thì \(\left( d \right)\) đi qua \(K\left( {1; – 1} \right)\)
Với \(a = – 4\) thì \(\left( d \right)\,:\,\,y = – 4x + 3\)
Đường thẳng \(\left( d \right)\) đi qua \(K\left( {1; – 1} \right)\) và \(H\left( {0;3} \right)\)
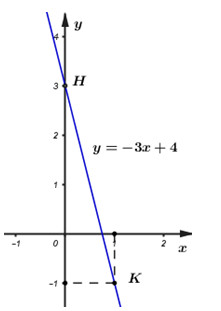
2) Tìm tất cả các giá trị của a để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.
Để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N\( \Leftrightarrow \,\,a \ne 0\)
\(M\left( {{x_M};{y_M}} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục Ox
\( \Rightarrow \left\{ \begin{array}{l}{y_M} = a{x_M} + 3\\{y_M} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = – \dfrac{3}{a}\\{y_M} = 0\end{array} \right.\)
\(\Rightarrow M\left( { – \dfrac{3}{a};0} \right) \Rightarrow OM = \left| { – \dfrac{3}{a}} \right| = \left| {\dfrac{3}{a}} \right|\)
\(N\left( {{x_N};{y_N}} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục Oy
\( \Rightarrow \left\{ \begin{array}{l}{y_N} = a{x_N} + 3\\{x_N} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = 0\\{y_M} = 3\end{array} \right.\)
\(\Rightarrow N\left( {0;3} \right) \Rightarrow ON = 3\)
Diện tích tam giác OMN bằng 4 \( \Rightarrow {S_{\Delta OMN}} = \dfrac{1}{2}OM.ON = \dfrac{1}{2}.\left| {\dfrac{3}{a}} \right|.3 = \dfrac{9}{2}.\left| {\dfrac{1}{a}} \right| = 4 \)
\(\Leftrightarrow \left| {\dfrac{1}{a}} \right| = \dfrac{8}{9} \Leftrightarrow \left| a \right| = \dfrac{9}{8} \Leftrightarrow \left[ \begin{array}{l}a = \dfrac{9}{8}\\a = – \dfrac{9}{8}\end{array} \right.\)
Vậy với \(a = \dfrac{9}{8}\) hoặc \(a = – \dfrac{9}{8}\)thỏa mãn yêu cầu đề bài.
3. Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếpđ).
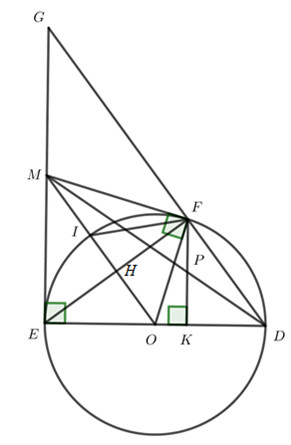
1) Chứng minh các điểm M, E, O, F cùng thuộc một đường tròn.
Vì MElà tiếp tuyến của \(\left( O \right)\) nên MEvuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1)
Vì MF là tiếp tuyến của \(\left( O \right)\) nên MFvuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO (2)
Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn.
2) Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác MEF.
Gọi \(MO \cap EF = \left\{ H \right\}\)
Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)
\( \Rightarrow ME = MF\) (tính chất) mà \(OE = OF = R\) (gt)
\( \Rightarrow \)MO là đường trung trực của EF
\( \Rightarrow MO \bot EF\)
\( \Rightarrow \angle IFE + \angle OIF = {90^o}\,\)
Vì \(OI = OF = R\) nên tam giác OIF cân tại O
\( \Rightarrow \angle OIF = \angle OFI\) mà \(\angle MFI + \angle OFI = {90^o}\,;\,\,\,\angle IFE + \angle OIF = {90^o}\)
\( \Rightarrow \angle MFI = \angle IFE\)
\( \Rightarrow \)FI là phân giác của \(\angle MFE\) (1)
Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)
\( \Rightarrow \)MI là phân giác của \(\angle EMF\) (tính chất) (2)
Từ (1) và (2) \( \Rightarrow \)I là tâm đường tròn nội tiếp tam giác MEF (đpcm)
3) Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Chứng minh P là trung điểm của FK.
Gọi G là giao điểm của tia DF và tia EM.
Ta có \(\angle EFD = {90^o}\)(góc nội tiếp chắn nửa đường tròn)\( \Rightarrow EF \bot DG\)mà \(EF \bot OM\) (cmt)
\( \Rightarrow OM//DG\) (từ vuông góc đến song song)
Tam giác EDG có \(OE = OD\,\,;\,\,OM//DG\,\, \Rightarrow ME = MG\)(tính chất đường trung bình)
Áp dụng định lý Ta-let cho tam giác EDM có \(PK//ME\) (cùng vuông góc với ED) ta được:\(\dfrac{{PK}}{{ME}} = \dfrac{{DP}}{{DM}}\) (3)
Áp dụng định lý Ta-let cho tam giác MDG có \(PF//MG\) (cùng vuông góc với ED) ta được: \(\dfrac{{PE}}{{MG}} = \dfrac{{DP}}{{DM}}\) (4)
Từ (3) và (4) suy ra \(\dfrac{{PK}}{{ME}} = \dfrac{{PF}}{{MG}}\) mà \(ME = MG\) (cmt)
\( \Rightarrow PK = PF\,\, \Rightarrow \)P là trung điểm của FK.
4. Giải phương trình \({x^2} + x – 17 = \sqrt {\left( {{x^2} – 15} \right)\left( {x – 3} \right)} + \sqrt {{x^2} – 15} + \sqrt {x – 3} \)
Điều kiện xác định \(\left\{ \begin{array}{l}{x^2} – 15 \ge 0\\x – 3 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge \sqrt {15} \\x \le – \sqrt {15} \end{array} \right.\\x \ge 3\end{array} \right. \Leftrightarrow x \ge \sqrt {15} \)
\(\begin{array}{l}\;\;\;\;{x^2} + x – 17 = \sqrt {\left( {{x^2} – 15} \right)\left( {x – 3} \right)} + \sqrt {{x^2} – 15} + \sqrt {x – 3} \\ \Leftrightarrow 2{x^2} + 2x – 34 = 2\sqrt {\left( {{x^2} – 15} \right)\left( {x – 3} \right)} + 2\sqrt {{x^2} – 15} + 2\sqrt {x – 3} \\ \Leftrightarrow {x^2} – 15 – 2\sqrt {\left( {{x^2} – 15} \right)\left( {x – 3} \right)} + x – 3 + {x^2} – 15 – 2\sqrt {{x^2} – 15} + 1 + x – 3 – 2\sqrt {x – 3} + 1 = 0\\ \Leftrightarrow {\left[ {\sqrt {{x^2} – 15} – \sqrt {x – 3} } \right]^2} + {\left[ {\sqrt {{x^2} – 15} – 1} \right]^2} + {\left[ {\sqrt {x – 3} – 1} \right]^2} = 0\end{array}\)
Ta thấy: \({\left[ {\sqrt {{x^2} – 15} – \sqrt {x – 3} } \right]^2} \ge 0\) với mọi \(x \ge \sqrt {15} \)
\({\left[ {\sqrt {{x^2} – 15} – 1} \right]^2} \ge 0\) với mọi \(x \ge \sqrt {15} \)
\({\left[ {\sqrt {x – 3} – 1} \right]^2} \ge 0\) với mọi \(x \ge \sqrt {15} \)
Vậy phương trình có nghiệm \( \Leftrightarrow {\left[ {\sqrt {{x^2} – 15} – \sqrt {x – 3} } \right]^2} = {\left[ {\sqrt {{x^2} – 15} – 1} \right]^2} = {\left[ {\sqrt {x – 3} – 1} \right]^2} = 0\)
Dấu “=” xảy ra \( \Leftrightarrow \sqrt {{x^2} – 15} = \sqrt {x – 3} = 1 \Leftrightarrow {x^2} – 15 = x – 3 = 1 \Leftrightarrow x = 4\)(tmđk)
Vậy nghiệm của phương trình là \(x = 4\)






