I. TRẮC NGHIỆM KHÁCH QUAN (2,0đ)
Chọn chữ cái đứng trước câu trả lời đúng và ghi vào tờ giấy thi của em.
1. :Căn bậc hai số học của \(16\) là
A.\(4\) B.\( – 4\)
C.\( \pm 4\) D.\(256\)
2. : Điều kiện xác định của biểu thức \(\sqrt {\dfrac{{2017}}{{x – 2018}}} \) là
A.\(x \ge 2018\) B.\(x \ne 2018\)
C.\(x > 2018\) D.\(x < 2018\)
3. : Rút gọn biểu thức \(\sqrt {7 – 4\sqrt 3 } + \sqrt 3 \) ta được kết quả là
A.\(2\) B.\(2\sqrt 3 – 2\)
C.\(2\sqrt 3 + 2\) D.\(2 – \sqrt 3 \)
4. : Hàm số \(y = (m – 2017)x + 2018\) đồng biến khi
A.\(m \ne 2017\) B.\(m \ge 2017\)
C.\(m > 2017\) D.\(m < 2017\)
5. : Tìm giá trị của \(m\) để đồ thị của hàm số \(y = (m – 2017)x + 2018\) đi qua điểm \((1\,;\,\,1)\) ta được
A.\(m = 2017\) B.\(m = 0\)
C.\(m > 2017\) D.\(m < 2017\)
6. : Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
A.\(\dfrac{3}{4}\) B.\(\dfrac{3}{5}\)
C.\(\dfrac{4}{3}\) D.\(\dfrac{4}{5}\)
7. :Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB = 9cm,\,\,BC = 15cm\). Khi đó độ dài \(AH\) bằng:
A.\(6,5cm\) B.\(7,2cm\)
C.\(7,5cm\) D.\(7,7cm\)
8. : Giá trị của biểu thức \(P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\) bằng
A.\(0\) B.\(1\)
C.\(2\) D.\(3\)
II. TỰ LUẬN (8,0đ):
Bài 1 (1,75đ): Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x – 3}} – \dfrac{{3x + 9}}{{x – 9}}\) với \(x \ge 0,\,\,x \ne 9\).
a) Rút gọn biểu thức \(P\).
b) Tính giá trị của biểu thức \(P\) tại \(x = 4 – 2\sqrt 3 \).
Bài 2 (2,0đ): Cho hàm số \(y = (m – 1)x + m\).
Advertisements (Quảng cáo)
a) Xác định giá trị của \(m\) để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng \(2\).
b) Xác định giá trị của \(m\) để đồ thị của hàm số cắt hoành tại điểm có hoành độ bằng \( – 3\).
c) Vẽ đồ thị của hai hàm số ứng với giá trị của \(m\) tìm được ở các câu a) và b) trên cùng hệ trục tọa độ \(Oxy\) và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
3. (3,0đ): Cho đường tròn \((O,R)\,\)và đường thẳng \(d\) cố định không cắt đường tròn. Từ một điểm \(A\) bất kì trên đường thẳng \(d\) kẻ tiếp tuyến \(AB\) với đường tròn (\(B\) là tiếpđ). Từ \(B\) kẻ đường thẳng vuông góc với \(AO\) tại \(H\), trên tia đối của tia \(HB\) lấy điểm \(C\) sao cho \(HC = HB\).
a) Chứng minh \(C\) thuộc đường tròn \((O,R)\,\)và \(AC\) là tiếp tuyến của đường tròn \((O,R)\,\).
b) Từ \(O\) kẻ đường thẳng vuông góc với đường thẳng \(d\) tại \(I\), \(OI\) cắt \(BC\) tại \(K\). Chứng minh \(OH.OA = OI.OK = {R^2}\).
c) Chứng minh khi \(A\) thay đổi trên đường thẳng \(d\) thì đường thẳng \(BC\) luôn đi qua một điểm cố định.
4. (1,25đ): a) Tìm giá trị nhỏ nhất của biểu thức \(Q = x – 2\sqrt {2x – 1} \).
b) Giải phương trình \(\sqrt {{x^2} – 3x + 2} + 3 = 3\sqrt {x – 1} + \sqrt {x – 2} \).
I. TRẮC NGHIỆM:
|
1. A |
2. C |
3. A |
4. C |
|
5. B |
6. D |
7. B |
8. C |
II. TỰ LUẬN: (7đ)
1. a) Với \(x \ge 0,\,\,x \ne 9\) ta có:
\(\begin{array}{l}P = \dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x – 3}} – \dfrac{{3x + 9}}{{x – 9}}\\\;\;\; = \dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x – 3}} – \dfrac{{3x + 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x – 3} \right)}}\\\;\;\; = \dfrac{{\sqrt x \left( {\sqrt x – 3} \right) + 2\sqrt x \left( {\sqrt x + 3} \right) – (3x + 9)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x – 3} \right)}}\\\;\;\; = \dfrac{{x – 3\sqrt x + 2x + 6\sqrt x – 3x – 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x – 3} \right)}}\\\;\;\; = \dfrac{{3\sqrt x – 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x – 3} \right)}}\\\;\;\; = \dfrac{{3\left( {\sqrt x – 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x – 3} \right)}}\\\;\;\; = \dfrac{3}{{\sqrt x + 3}}.\end{array}\)
Vậy \(P = \dfrac{3}{{\sqrt x + 3}}\) với \(x \ge 0,\,\,x \ne 9\)
b) Theo câu a) với \(x \ge 0,\,\,x \ne 9\)ta có \(P = \dfrac{3}{{\sqrt x + 3}}\).
Ta có \(x = 4 – 2\sqrt 3 \)thỏa mãn ĐKXĐ.
Có: \(x = 4 – 2\sqrt 3 = 3 – 2.\sqrt 3 .1 + 1 = {\left( {\sqrt 3 – 1} \right)^2}\)
\( \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt 3 – 1} \right)}^2}} = \left| {\sqrt 3 – 1} \right| = \sqrt 3 – 1.\)
Thay \(\sqrt x = \sqrt 3 – 1\)vào biểu thức ta có:
Advertisements (Quảng cáo)
\(\begin{array}{l}P = \dfrac{3}{{\sqrt 3 – 1 + 3}} = \dfrac{3}{{\sqrt 3 + 2}} = \dfrac{{3\left( {2 – \sqrt 3 } \right)}}{{\left( {2 + \sqrt 3 } \right)\left( {2 – \sqrt 3 } \right)}}\\\;\;\; = \dfrac{{6 – 3\sqrt 3 }}{{4 – 3}} = 6 – 3\sqrt 3 .\end{array}\)
Vậy \(P = 6 – 3\sqrt 3 \) khi\(x = 4 – 2\sqrt 3 \).
2. a) Đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng \(2\) nên đồ thị của hàm số đi qua điểm \(A(0\,;\,\,2)\)
\( \Leftrightarrow 2 = (m – 1).0 + m \Leftrightarrow m = 2\)
Vậy với \(m = 2\) thì đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng \(2\).
b) Đồ thị của hàm số cắt trục hoành tại điểm của hoành độ bằng \( – 3\) nên đồ thị của hàm số đi qua điểm \(B( – 3\,;\,\,0)\)
\(\begin{array}{l} \Leftrightarrow 0 = (m – 1).( – 3) + m \Leftrightarrow 0 = – 3m + 3 + m\\ \Leftrightarrow 2m = 3 \Leftrightarrow m = \dfrac{3}{2}\end{array}\)
Vậy với \(m = \dfrac{3}{2}\) thì đồ thị của hàm số cắt trục hoành tại điểm của hoành độ bằng \( – 3\).
c) +) Với \(m = 2\) hàm số trở thành \(y = x + 2\).
+) Với \(m = \dfrac{3}{2}\) hàm số trở thành \(y = \dfrac{1}{2}x + \dfrac{3}{2}\).
Ta có bảng giá trị:
|
\(x\) |
0 |
1 |
|
\(y = x + 2\) |
2 |
3 |
|
\(y = \dfrac{1}{2}x + \dfrac{3}{2}\) |
\(\dfrac{3}{2}\) |
2 |
Đồ thị của hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \((1\,;\,\,3)\) và \((0\,;\,\,2)\).
Đồ thị của hàm số \(y = \dfrac{1}{2}x + \dfrac{3}{2}\) là đường thẳng đi qua hai điểm \(\left( {0\,;\,\,\dfrac{3}{2}} \right)\) và \((1\,;\,\,2)\).
+) Vẽ đồ thị của hai hàm số:
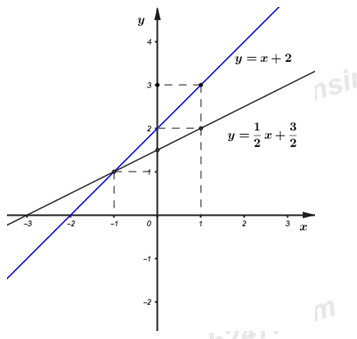
+) Tìm tọa độ giao điểm của hai đồ thị hàm số.
Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình:
\(\begin{array}{l}\;\;\;\;x + 2 = \dfrac{1}{2}x + \dfrac{3}{2} \Leftrightarrow x – \dfrac{1}{2}x = \dfrac{3}{2} – 2\\ \Leftrightarrow \dfrac{1}{2}x = \dfrac{{ – 1}}{2} \Leftrightarrow x = – 1\end{array}\)
Với \(x = – 1\) ta được \(y = – 1 + 2 = 1\).
Vậy tọa độ giao điểm của hai đường thẳng là \(( – 1\,;\,\,1)\).
3.
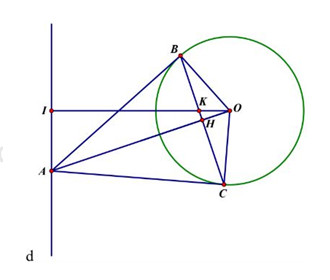
a) +) Chứng minh \(C\) thuộc đường tròn \(\left( O \right):\)
Xét \(\Delta BHO\) và \(\Delta CHO\) ta có:
\(\begin{array}{l}OH\;\;chung\\\angle OHB = \angle OHC = {90^0}\\BH = HC\;\left( {gt} \right)\\ \Rightarrow \Delta BHO = \Delta CHO\;\;\left( {c – g – c} \right).\end{array}\)
\( \Rightarrow OB = OC = R\) (hai cạnh tương ứng)
\( \Rightarrow C\) thuộc đường tròn \(\left( O \right).\) (đpcm)
+) Chứng minh \(AC\) là tiếp tuyến của đường tròn \(\left( O \right):\)
Ta có: \(\Delta BHO = \Delta CHO\;\;\left( {cmt} \right) \Rightarrow \angle BOH = \angle COH\) (hai góc tương ứng).
Xét \(\Delta ABO\) và \(\Delta ACO\) ta có:
\(\begin{array}{l}BO = OC\;\left( { = R} \right)\\\angle BOA = \angle COA\;\;\left( {cmt} \right)\\OA\;\;chung\\ \Rightarrow \Delta ABO = \Delta ACO\;\;\left( {c – g – c} \right).\end{array}\)
\( \Rightarrow \angle ABO = \angle ACO = {90^0}\) (hai góc tương ứng)
Hay \(OC \bot AC\)
\( \Rightarrow AC\)là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(C.\) (đpcm)
b) Xét \(\Delta OHK\) và \(\Delta OIA\) ta có:
\(\begin{array}{l}\angle KOH\;\;chung\\\angle OIA = \angle OHK = {90^0}\\ \Rightarrow \Delta OHK \sim \Delta OIA\;\;\left( {g – g} \right)\end{array}\)
\( \Rightarrow \dfrac{{OH}}{{OI}} = \dfrac{{OK}}{{OA}} \Rightarrow OH.OA = OK.OI\) (các cặp cạnh tương ứng tỉ lệ)
Xét \(\Delta ABO\)vuông tại \(B\) có đường cao\(BH\)ta có:
\(\begin{array}{l} \Rightarrow B{O^2} = OH.OA\,\,\, \Rightarrow OH.OA = {R^2}\\ \Rightarrow OH.OA = OI.OK = {R^2}\;\;\;\left( {dpcm} \right).\end{array}\)
c) Theo câu b) ta có: \(OI.OK = {R^2}\,\, \Rightarrow OK = \dfrac{{{R^2}}}{{OI}}\)không đổi.
Mà \(K\) thuộc \(OI\) cố định nên \(K\) cố định.
Vậy khi \(A\)thay đổi trên đường thẳng \(d\) thì đường thẳng \(BC\) luôn đi qua điểm \(K\) cố định.
4. a) Điều kiện: \(x \ge \dfrac{1}{2}\).
Ta có: \(Q = x – 2\sqrt {2x – 1} \)
\(\begin{array}{l} \Rightarrow 2Q = 2\left( {x – 2\sqrt {2x – 1} } \right) = 2x – 4\sqrt {2x – 1} = 2x – 1 – 4\sqrt {2x – 1} + 4 – 3\\ \Rightarrow 2Q = {\left( {\sqrt {2x – 1} – 2} \right)^2} – 3 \ge – 3\\ \Rightarrow Q \ge \dfrac{{ – 3}}{2}\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \sqrt {2x – 1} – 2 = 0 \) \(\Leftrightarrow \sqrt {2x – 1} = 2 \) \(\Leftrightarrow 2x – 1 = 4 \Leftrightarrow x = \dfrac{5}{2}\;\left( {tm} \right)\)
Vậy giá trị nhỏ nhất của biểu thức \(Q = x – 2\sqrt {2x – 1} \) là \(Q = \dfrac{{ – 3}}{2}\) khi \(x = \dfrac{5}{2}.\)
b) ĐKXĐ: \(x \ge 2\) .
Với \(x \ge 2\) ta có:
\(\begin{array}{l}\;\;\;\;\;\sqrt {{x^2} – 3x + 2} + 3 = 3\sqrt {x – 1} + \sqrt {x – 2} \\ \Leftrightarrow \sqrt {(x – 1)(x – 2)} + 3 – 3\sqrt {x – 1} – \sqrt {x – 2} = 0\\ \Leftrightarrow \sqrt {x – 1} \left( {\sqrt {x – 2} – 3} \right) – \left( {\sqrt {x – 2} – 3} \right) = 0\\ \Leftrightarrow \left( {\sqrt {x – 2} – 3} \right)\left( {\sqrt {x – 1} – 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {x – 2} – 3 = 0\\\sqrt {x – 1} – 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {x – 2} = 3\\\sqrt {x – 1} = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x – 2 = 9\\x – 1 = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 11\\x = 2\end{array} \right.\end{array}\).
Ta thấy \(x = 11\) và \(x = 2\) thỏa mãn ĐKXĐ.
Vậy tập nghiệm của phương trình là \(S = {\rm{\{ 11}}\,{\rm{;}}\,\,{\rm{2\} }}\).
