Đề thi học kì 1 Toán lớp 9: Chứng minh bốn điểm B, K, H, A cùng thuộc một đường tròn

Bài 1: (2đ) Thực hiện phép tính (thu gọn):

1) \(2\sqrt {48}  + \dfrac{1}{3}\sqrt {108}  – 5\sqrt 3  – 3\sqrt {27} \).

2) \(\dfrac{{6 – \sqrt 6 }}{{\sqrt 6  – 1}} – 9\sqrt {\dfrac{2}{3}}  – \dfrac{4}{{2 – \sqrt 6 }}\).

Bài 2: (1đ)Giải phương trình: \(\dfrac{5}{3}\sqrt {9x – 18}  – \dfrac{1}{2}\sqrt {16x – 32}  – 15 = 0\).

Bài 3: (1,75đ) Cho hàm số \(y = 3x\) có đồ thị \(\left( D \right)\) và hàm số \(y = x + 2\) có đồ thị \(\left( {{D_1}} \right)\).

1) Vẽ \(\left( D \right)\)và \(\left( {{D_1}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\).

2) Tìm \(m\) để đường thẳng \(y = \left( {m – 5} \right)x + m + 2\) có đồ thị \(\left( {{D_2}} \right)\) cắt \(\left( {{D_1}} \right)\)tại điểm B có hoành độ bằng 2.

Bài 4: (3,25đ) Cho  tam giác ABC vuông tại A, đường tròn \(\left( O \right)\)đường kính ACcắtBC tại K, vẽ dây cung ADcủa \(\left( O \right)\) vuông góc với BOtạiH.

1) Chứng minh bốn điểm B, K, H, A cùng thuộc một đường tròn.

2) Chứng minh: BD là tiếp tuyến của đường tròn \(\left( O \right)\)

3) Chứng minh \(BH.BO = BK.BC\).

4) Từ \(\left( O \right)\)vẽ đường thẳng song song với AD cắt tia BA tại E, từ B vẽ đường thẳng vuông góc với EC tại F, BF cắt AO tại M. Chứng minh: \(MA = MO\)

Bài 5: (1đ) Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc \({70^o}\)thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học, Bình hãy giúp Ba tính chiều dài thang là bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ nhất)

Bài 6: (1đ)  Tháng 11 vừa qua có ngày Black Friday, phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mua một đôi giày. Biết đôi giày đang khuyến mại giảm giá 40%, mẹ bạn An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm nữa, do đó mẹ bạn An phải trả 684.000 đ cho đôi giày. Hỏi giá ban đầu của đôi giày nếu không khuyến mại là bao nhiêu?

Bài 1:Thực hiện phép tính (thu gọn):

\(\begin{array}{l}1)\;2\sqrt {48}  + \dfrac{1}{3}\sqrt {108}  – 5\sqrt 3  – 3\sqrt {27} \\ = 2.\sqrt {{4^2}.3}  + \dfrac{1}{3}\sqrt {{6^2}.3}  – 5\sqrt 3  – 3.\sqrt {{3^2}.3} \\ = 8\sqrt 3  + 2\sqrt 3  – 5\sqrt 3  – 9\sqrt 3  =  – 4\sqrt 3 \end{array}\)

Vậy \(2\sqrt {48}  + \dfrac{1}{3}\sqrt {108}  – 5\sqrt 3  – 3\sqrt {27}  =  – 4\sqrt 3 \).

\(\begin{array}{l}2)\;\dfrac{{6 – \sqrt 6 }}{{\sqrt 6  – 1}} – 9\sqrt {\dfrac{2}{3}}  – \dfrac{4}{{2 – \sqrt 6 }}\\ = \dfrac{{\sqrt 6 .\sqrt 6  – \sqrt 6 }}{{\sqrt 6  – 1}} – 3.{\left( {\sqrt 3 } \right)^2}\dfrac{{\sqrt 2 }}{{\sqrt 3 }} – \dfrac{{4\left( {2 + \sqrt 6 } \right)}}{{\left( {2 – \sqrt 6 } \right)\left( {2 + \sqrt 6 } \right)}}\\ = \dfrac{{\sqrt 6 \left( {\sqrt 6  – 1} \right)}}{{\sqrt 6  – 1}} – 3.\sqrt 3 .\sqrt 2  – \dfrac{{4\left( {2 + \sqrt 6 } \right)}}{{{2^2} – {{\left( {\sqrt 6 } \right)}^2}}}\\ = \sqrt 6  – 3\sqrt 6  – \dfrac{{4\left( {2 + \sqrt 6 } \right)}}{{ – 2}}\\ =  – 2\sqrt 6  + 2\left( {2 + \sqrt 6 } \right) = 4\end{array}\).

Vậy \(\dfrac{{6 – \sqrt 6 }}{{\sqrt 6  – 1}} – 9\sqrt {\dfrac{2}{3}}  – \dfrac{4}{{2 – \sqrt 6 }} = 4\).

Bài 2:Giải phương trình: \(\dfrac{5}{3}\sqrt {9x – 18}  – \dfrac{1}{2}\sqrt {16x – 32}  – 15 = 0\).

ĐKXĐ: \(x \ge 2\). Với điều kiện này ta có:

\(\begin{array}{l}\;\;\;\;\;\dfrac{5}{3}\sqrt {9x – 18}  – \dfrac{1}{2}\sqrt {16x – 32}  – 15 = 0\\ \Leftrightarrow \dfrac{5}{3}\sqrt {{3^2}\left( {x – 2} \right)}  – \dfrac{1}{2}\sqrt {{4^2}\left( {x – 2} \right)}  = 15\\ \Leftrightarrow 5\sqrt {x – 2}  – 2\sqrt {x – 2}  = 15\\ \Leftrightarrow 3\sqrt {x – 2}  = 15 \Leftrightarrow \sqrt {x – 2}  = 5\\ \Leftrightarrow {\left( {\sqrt {x – 2} } \right)^2} = {5^2} \Leftrightarrow x – 2 = 25\\ \Leftrightarrow x = 27\end{array}\)

Nhận thấy \(x = 27\) thỏa mãn ĐKXĐ

Vậy \(x = 27\)là nghiệm của phương trình.

Bài 3:Cho hàm số \(y = 3x\) có đồ thị \(\left( D \right)\) và hàm số \(y = x + 2\) có đồ thị \(\left( {{D_1}} \right)\).

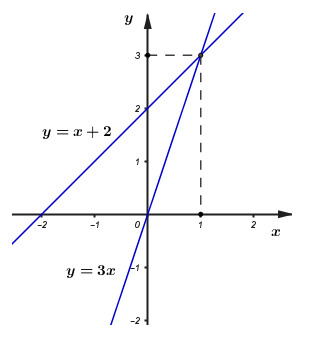
1)Vẽ \(\left( D \right)\)và \(\left( {{D_1}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\).

Ta có bảng giá trị:

Vậy đường thẳng \(\left( D \right)\) đi qua 2 điểm \(\left( {0;\;0} \right),\;\;\left( {1;\;3} \right)\) và

đường thẳng \(\left( {{D_1}} \right)\) đi qua 2 điểm \(\left( {0;\;2} \right),\;\;\left( {1;\;3} \right).\)

Từ đó ta có đồ thị của hai hàm số như hình bên:

2)Tìm \(m\) để đường thẳng \(y = \left({m – 5} \right)x + m + 2\) có đồ thị \(\left( {{D_2}} \right)\) cắt \(\left( {{D_1}} \right)\)tại điểm B có hoành độ bằng 2.

Vì điểm B có hoành độ bằng 2 và thuộc \(\left( {{D_1}} \right)\)nên ta có tung độ điểm B là: \(y = x + 2 = 2 + 2 = 4\).

Thay tọa độ điểm \(B\left( {2;4} \right)\) vào phương trình \(y = \left( {m – 5} \right)x + m + 2\;\;\left( {{D_2}} \right)\) có:

\(2\left( {m – 5} \right) + m + 2 = 4 \)

\(\Leftrightarrow 2m – 10 + m + 2 = 4\)

\(\Leftrightarrow 3m = 12 \Leftrightarrow m = 4\).

Vậy \(m = 4\)là giá trị cần tìm.

Bài 4:Cho  tam giác ABC vuông tại A, đường tròn \(\left( O \right)\)đường kính AC cắt BC tại K, vẽ dây cung AD của \(\left( O \right)\) vuông góc với BO tại H.

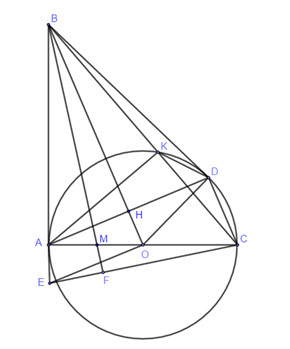
1)Chứng minh bốn điểm B, K, H, A cùng thuộc một đường tròn.

Ta có:  \(\Delta AKC\) thuộc đường tròng \(\left( O \right)\) có đường kính \(AC \Rightarrow \Delta AKC\) vuông tại \(K \Rightarrow \angle BKA = {90^0}.\)

\( \Rightarrow B,\;K,\;A\) cùng thuộc đường tròn đường kính \(BA.\;\;\;\left( 1 \right)\)

Lại có: \(BO \bot AD = \left\{ H \right\} \Rightarrow \angle BHA = {90^0}\)

\( \Rightarrow B,\;H,\;A\) cùng thuộc đường tròn đường kính \(BA\;\;\;\left( 2 \right)\)

Từ (1) và (2) suy ra \(B,H,\;A,\;K\) cùng thuộc đường tròn đường kính \(BA.\)  (đpcm)

2)Chứng minh: BD là tiếp tuyến của đường tròn \(\left( O \right)\)

Xét tam giác cân OADcân tại O (do \(OA = OD = R\)) có: OB vuông góc với AD

Suy ra OB  đồng thời cũng là trung trực của cạnh AD (tính chất tam giác cân)

Suy ra \(AB = BD\)(tính chất trung trực)

Xét tam giác ABOvà tam giác DBO có:

+) \(AB = BD\) (cmt)

+) \(AO = OD\) (cùng là bán kính của đường tròn)

+) BO chung

\( \Rightarrow \Delta ABO = \Delta DBO\left( {c – c – c} \right) \)

\(\Rightarrow \angle BDO = \angle BAO = {90^o}\) \( \Rightarrow BD \bot OD\)

Suy ra BD là tiếp tuyến của đường tròn \(\left( O \right)\)(đpcm).

3)Chứng minh \(BH.BO = BK.BC\).

Xét tam giác vuông BODvuông tại Dcó HDlà đường cao

\( \Rightarrow BH.BO = H{D^2}\) (hệ thức lượng trong tam giác vuông)  (1)

Xét tam giác BDK và tam giác BCD có:

+) \(\angle CBD\) chung

+) \(\angle BDK = \angle BCD\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung DK)

\( \Rightarrow \Delta BDK \sim \Delta BCD\;\;\left( {g – g} \right) \)

\(\Rightarrow \dfrac{{BD}}{{BC}} = \dfrac{{BK}}{{BD}} \Rightarrow BK.BC = B{D^2}\) (2)

Từ (1) và (2) suy ra \(BH.BO = BK.BC\)(đpcm).

4) Từ \(\left( O \right)\)vẽ đường thẳng song song với AD cắt tia BA tại E, từ B vẽ đường thẳng vuông góc với EC tại F, BF cắt AO tại M. Chứng minh: \(MA = MO\)

Xét tam giác BEF và tam giác CEA có:

+) \(\angle ABM = \angle ACE\) (do cùng phụ với \(\angle BEC\))

+) \(\angle CAE = \angle BAM = {90^o}\)

\( \Rightarrow \Delta BAM \sim \Delta CAE\;\left( {g – g} \right)\)

\(\Rightarrow \dfrac{{AM}}{{AE}} = \dfrac{{AB}}{{AC}} \)

\(\Rightarrow AB.AE = AM.AC\)      (3)

Xét tam giác BOE vuông tại O có AO là đường cao\( \Rightarrow AB.AE = A{O^2}\)    (4)

Từ (3) và (4) \( \Rightarrow A{O^2} = AM.AC\)

\(\Leftrightarrow A{O^2} = 2AO.AM \)

\(\Leftrightarrow 2AM = AO\)

Mà có \(AM + MO = AO\)

\(\Rightarrow MO = AO – AM = 2AM – AM = AM\).

Vậy \(AM = MO\) (đpcm)\(\)\(\)

Bài 5:Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc \({70^o}\)thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học, Bình hãy giúp ba tính chiều dài thang là bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ nhất)

Ta có hình vẽ minh họa:

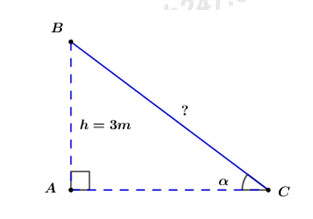
Như vậy độ dài cạnh BC chính là chiều dài của chiếc thang.

Xét tam giác ABC vuông tại A có:

\(\sin \alpha  = \dfrac{{AB}}{{BC}} \) \(\Rightarrow BC = \dfrac{{AB}}{{\sin \alpha }} = \dfrac{3}{{\sin {{70}^o}}} = 3,19m\)

Vậy chiều dài của chiếc thang cần làm là \(3,19m\).

Bài 6:Tháng 11 vừa qua có ngày Black Friday, phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mua một đôi giày. Biết đôi giày đang khuyến mại giảm giá 40%, mẹ bạn An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm nữa, do đó mẹ bạn An phải trả 684.000 đ cho đôi giày. Hỏi giá ban đầu của đôi giày nếu không khuyến mại là bao nhiêu?

Gọi số tiền ban đầu của đôi giày là \(A\;\left( {A > 684.000} \right)\)(đồng).

Vì đôi giày đang khuyến mại giảm giá 40% nên giá tiền của đôi giày là: \(A – A.40\%  = 0,6A\)

Vì mẹ bạn An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm nữa nên giá tiền của đôi giày là: \(0,6A – 0,6A.5\%  = 0,57A\)

Vì mẹ bạn An phải trả 684.000 đ cho đôi giày nên ta có:

\(0,57A = 684000 \) \(\Rightarrow A = \dfrac{{684000}}{{0,57}} = 1200000\;\;\left( {tm} \right)\) (đồng)

Vậy số tiền ban đầu của đôi giày là 1.200.000 đồng