Bài 1,2,3,4,5 trang 66,67 SGK Toán 8 tập 1: Tứ giác

Tứ giác: giải bài 1,2 trang 66; Bài 3,4,5 trang 67 SGK Toán 8 tập 1 Chương 1.

Bài 1. Tìm x ở hình 5, hình 6:

Ở hình 5:

• Hình 5a) Xét ABCD có ∠A + ∠B + ∠C + ∠D = 360⁰  ⇒ x = 360⁰ – (110⁰ + 120⁰ + 80⁰) = 50⁰
• Hình 5b) Xét EFGH có: ∠E + ∠F + ∠G + ∠H = 360⁰  ⇒ x = 360⁰­ – (90⁰ +90⁰+ 90⁰) = 90⁰
• Hình 5c) Xét ABDE có: ∠A + ∠B + ∠D + ∠E = 360⁰  ⇒ 65⁰ +  90⁰ + x + 90⁰ ⇒ x = 360⁰­ – (90⁰ + 90⁰ + 65⁰) = 115⁰
• Hình 5d)  Xét IKNM có:∠I + ∠K+ ∠M + ∠N = 360⁰ ⇒ x = 360⁰ – (75⁰ + 120⁰ +90⁰) = 75⁰   vì ∠K = 180⁰ – 60⁰ =120⁰    ∠M = 180⁰ – 105⁰ = 75⁰

Ở hình 6.

Hình 6a) Xét PQRS có :∠P + ∠Q+ ∠R + ∠S= 360⁰ ⇒ x+ x+ 65⁰ + 95⁰ = 360⁰ ⇒ 2x = 360⁰ – (65⁰ + 95⁰) ⇒

⇒ x =100⁰

Hình 6b)  Xét MNPQ có: ∠M + ∠N + ∠P + ∠Q = 360⁰ ⇒ 3x+4x+x+2x = 360⁰  ⇒ 2x + 3x + 4x + x = 360⁰

⇒ 10x = 360⁰

⇒ x = 36⁰

---

Bài 2 trang 66. Góckề bù với một góc của tứ giác gọi là góc ngoài của tứgiác.

a) Tính các góc ngoài của tứgiác ở hình 7a.

b) Tính tổng các gócngoài của tứgiác ở hình 7b (tại mỗi đỉnh của tứgiác chỉ chọn một gócngoài) :∠A₁ + ∠B₁  + ∠C₁ + ∠D₁=?

c) Có nhận xét gì về tổng các gócngoài của tứgiác?

HD.Giải: a) Gócngoài còn lại: ∠D=360⁰ – (75⁰ + 90⁰ + 120⁰) = 75⁰

Ta tính được các gócngoài tại các đỉnh A, B, C, D lần lượt là:

Ta có: ∠A₁=105⁰, ∠B₁₌ 90⁰, ∠C₁₌60⁰, ∠D₁₌105⁰

b)Hình 7b SGK:

Tổng các góctrong ∠A + ∠B  + ∠C + ∠D=360⁰

Nên tổng các góc ngoài  ∠A₁ + ∠B₁  + ∠C₁ + ∠D₁=(180⁰ – ∠A) + (180⁰ – ∠B) +  (180⁰ – ∠C) +  (180⁰ – ∠D) = (4.180⁰ – (∠A + ∠B  + ∠C + ∠D)= 720⁰ – 360⁰ = 360⁰

c) Nhận xét: Tổng các góc ngoài của tứ-giác bằng 360⁰ 

---

Bài 3 trang 67. Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình “cái diều”

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính ∠B, ∠D biết rằng ∠A= 100⁰ và ∠C= 60⁰ .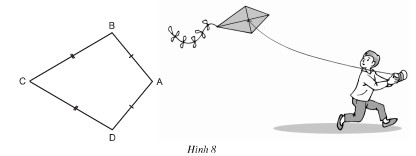

Giải: Ta có: AB = AD (gt)  => A thuộc đường trung trực của BD

CB = CD (gt)   => C thuộc đường trung trực của BD.

Vậy AC là đường trung trực của BD.

b) 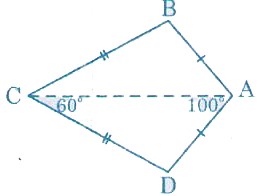Xét ∆ ABC và ∆ADC có AB = AD (gt)

BC = DC (gt)

AC cạnh chung

nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ∠B = ∠D, Ta có ∠B + ∠D = 360⁰ – (100⁰ + 60⁰) = 200⁰

Do đó ∠B = ∠D = 200⁰ /2 = 100⁰

---

Bài 4 trang 67 Toán 8 tập 1. Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ-giác ở hình 9, hình 10 vào vở.

 Vẽ lại các tứ-giác ở hình 9, hình 10 sgk vào vở

(*) Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).

– Vẽ đoạn thẳng AC = 3cm.

– Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.

– Hai cung tròn trên cắt nhau tại B.

– Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.

Tương tự ta sẽ được tam giác ACD.

Tứgiác ABCD là tứgiác cần vẽ.

(*) Cách vẽ hình 10:

Dùng thước đo góc vẽ ∠xAy= 70⁰

– Trên tia Ax lấy điểm D sao cho AD = 4cm

– Trên tia Ay lấy điểm B sao cho AB = 2cm

– Vẽ đoạn thẳng BD

– Lần lượt lấy B,D là tâm vẽ cùng phía các cung tròn có bán kính BC =1,5 cm và DC= 3cm đối với đường thẳng BD(Khác phía đối với điểm A). Hai cung tròn đó cắt nhau tại điểm C.

– Vẽ các đoạn thẳng BC, DC ta được hình 10.

---

Bài 5 Toán 8 tập 1 – Hình học

Đố. 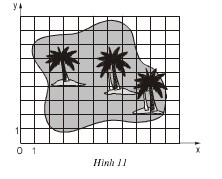Đố em tìm thấy vị trí của “kho báu” trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứgiác ABCD, trong đó các đỉnh của tứ-giác có tọa độ như sau: A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).

Các bước làm như sau:

– Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).

– Vẽ tứ-giác ABCD.

– Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.

– Xác định tọa độ của điểm K: K(5 ; 6)

Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ.