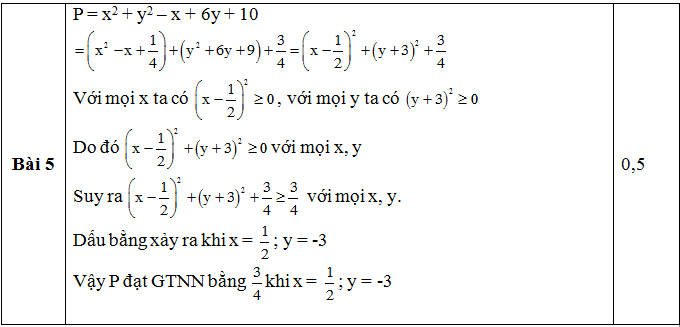Đề và đáp án của thầy Lê Văn Hà gửi: KSCL đầu năm Toán 8 2015 trường THCS Võ Thị Sáu – Hải Phòng.
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM
MÔN TOÁN 8 – NĂM HỌC 2015 – 2016
Thời gian làm bài 90 phút
(không tính thời gian giao đề)
Bài 1 (3, 0 điểm).
a/ Thu gọn đa thức A(x) = 5x3 + 2x4 – x2+ 3x2 – x3 – x4+ 1- 4x3
b/ Tính M(1) , M(-1) với M(x) = x4 + 2x2 + 1
c/ Chứng minh rằng đa thức M(x) = x4 + 2x2 + 1 không có nghiệm.
Advertisements (Quảng cáo)
Bài 2 (2, 0 điểm). Rút gọn các biểu thức sau:
a/ 2x2(1 – 3x) + 6x3
b/ (x – y)2 +(x + y)2 +2(x – y)(x + y)
Bài 3 (1, 0 điểm).
Advertisements (Quảng cáo)
Tìm x biết : 2x(x – 5) – x(3 + 2x) = 26
Bài 4 (3, 5 điểm).
Cho tam giác ABC có góc A=900 , đường phân giác BD (D∈AC). Qua D kẻ DE vuông góc với BC (E∈BC).
a/ Chứng minh DABD = DEBD
b/ Chứng minh BD là đường trung trực của đoạn thẳng AE.
c/ Gọi K là giao điểm của AB và DE. Chứng minh DK = DC.
d/ Tứ giác AECK là hình gì? Vì sao?
Bài 5 (0, 5 điểm).
Tìm giá trị nhỏ nhất của đa thức và giá trị của x và y tương ứng.
P = x2 + y2 – x + 6y + 10
————————Hết————————–
Đáp án đề KSCL đầu năm môn Toán 8 trường THCS Võ Thị Sáu – Hải Phòng năm học 2015-2016
| Bài | Đáp án | Điểm |
| Bài 1 | a/ A(x) = 5x3 + 2x4 – x2+ 3x2 – x3 – x4+ 1- 4x3
=( 5x3 – x3 – 4x3) + (2x4 – x4) + (– x2 + 3x2) + 1 = x4 + 2x2 + 1 |
0,5 0,5 |
| b/ M(1) = 14 + 2. 12 + 1 = 4
M(-1) = (-1)4 + 2. (-1)2 + 1 = 4 |
0,5
0,5 |
|
| c/ Với mọi x thì x4 ≥ 0; 2x2 ≥ 0
Suy ra x4 + 2x2 + 1 ≥ 1 > 0 với mọi x Vậy đa thức M(x) không có nghiệm. |
0,25
0,25 0,5 |
|
| Bài 2 | a/ 2x2(1 – 3x) + 6x3 = 2x2 – 6x3 + 6x3 = 2x2 | 1,0 |
| b/Gọi A = (x – y)2 +(x + y)2 +2(x – y)(x + y)
Đặt a = x – y ; b = x + y Biểu thức A= a2 + b2 + 2ab = (a + b)2 Thay a = x – y ; b = x + y vào A ta được A = [(x-y) +(x+y)]2 = [x-y+x+y]2 = (2x)2 = 4x2 |
1, 0 |
|
| Bài 3 | Thực hiện phép tính vế trái ta được 2x2 – 10x – 3x – 2x2 = -13x
Ta phải tìm x biết -13x = 26, từ đó x = -2 |
0,5
0,5 |
| Bài 4 |  |
0,5 |
| a/ Dễ dàng chứng minh ΔDABD = ΔDEBD (c. c. c) | 0,75 | |
| b/ Vì ΔDABD = ΔDEBD nên BA = BE, DA = DE
Hai điểm B và D cách đều 2 mút của đoạn thẳng AE do đó BD là đường trung trực của đoạn thẳng AE. |
0,75 |
|
| c/ Dễ dàng chứng minh ΔDADK = ΔDEDC (∠ADK = ∠DEC =900 ,DA = DE, ∠ADK=∠EDC), , suy ra DK = DC |
1, 0 |
|
| d/ Xét DBKC có KE ⊥ BC (gt); CA ⊥ BK (gt) mà KE cắt CA tại D nên D là trực tâm của DBKC suy ra BD ⊥ KC.
Lại có BD ⊥ AE ( vì BD là đường trung trực của đoạn thẳng AE ) do đó AE // CK (1) Mặt khác từ DA = DE và DC = DK (cmt) nên DA + DC = DE + DK hat AC = KE (2) Từ (1) và (2) suy ra tứ giác AECK là hình thang cân. |
0,25 0,25 |