Dethikiemtra.com gửi tới thầy cô và các em Đề kiểm tra chất lượng giữa HK1 môn Toán 8 trường THCS Bối Cầu.
| PHÒNG GD & ĐT BÌNH LỤC
Trường THCS Bối Cầu |
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
Năm học: 2015-2016 Môn: Toán. Lớp 8 Thời gian làm bài 90 phút. |
1: (2,0 điểm) Thực hiện phép tính:
a) 2x2 (3x2 – xy – 3/2y2)
b) (16x4y3 – 20x2y3 – 4x4y4) : 4x2y2
2: (3,0 điểm) Phân tích đa thức thành nhân tử :
a) 5x(3 – 2x) – 7 (2x -3)
b) x3 – 4x2 + 4x
Advertisements (Quảng cáo)
c) x2 + 5x + 6
3: (2,0 điểm) Cho biểu thức:
M = (4x + 3)2 – 2x(x + 6) – 5(x -2)(x +2)
Advertisements (Quảng cáo)
a) Thu gọn biểu thức M.
b) Tính giá trị biểu thức tại x = -2
c) Chứng minh biểu thức M luôn dương.
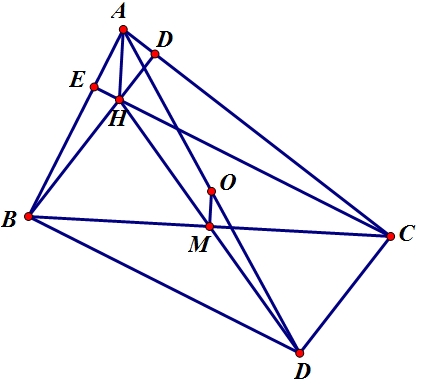
4: (3 điểm) Cho tam giác ABC, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở
D.Chứng minh rằng:
a) BDCH là hình bình hành.
b) ∠BAC + ∠BDC = 1800
c) H, M, D thẳng hàng ( M là trung điểm của BC)
d) OM = 1/2AH ( O là trung điểm của AD)
| Câu |
Hướng dẫn chấm |
Điểm |
| 1
( 2 đ) |
a) Thực hiện phép tính
2x2 (3x2 – xy – 3/2y2) = 2x2.3x2 – 2x2.(-xy) -2x2.(-3/2y2) = 6x4 + 2x3y +3x2y2 |
0.5 0.5 |
| b) (16x4y3 – 20x2y3 – 4x4y4) : 4x2y2.
= (16x4y3: 4x2y2) – (20x2y3: 4x2y2 ) – (4x4y4: 4x2y2) = 4x2y – 5y – x2y2 |
0.5 0.5
|
|
| 2
( 3 đ) |
Phân tích đa thức sau thành nhân tử.
a) 5x (3 -2x) – 7(2x – 3) = 5x ( 3 -2x) + 7(3 -2x) = (3 -2x)(5x + 7)
|
0.5 0.5 |
| b) x3– 4x2 + 4x
= x(x2 – 4x +4) = x(x-2)2 |
0.5 0.5 |
|
| c) x2 + 5x + 6
= (x2 + 2x) + (3x + 6) = x(x+2) + 3(x+2) = (x+2)(x+3) |
0.5 0.5
|
|
| 3
( 2 đ) |
a) M = (4x + 3)2 – 2x(x + 6) – 5(x -2)(x +2)
= 16x2 + 24x + 9 – 2x2 – 12x – 5x2 + 20 = 9 x2 + 12x + 29 |
0,25
0,25 0,25 |
| b) Thay x = -2 vào M ta có M = 9 (-2)2 + 12 (-2) +29
= 36 -24 +29 = 41 Vậy x = -2 thì M = 41 |
0,25
0,25 0,25 |
|
| c)Ta có: M = 9 x2 + 12x + 29 = ( 3x +2)2 + 25
Vì ( 3x +2)2 ≥ 0 với mọi x 25 > 0 nên M ≥ 25 Do đó M > 0 với mọi x |
0,25
0,25 |
|
| 4
( 3 đ)
|
 |
|
| a)BH // DC ( cùng vuông góc với AC )
CH // DB ( cùng vuông góc với AB) nên BDCH là HBH. |
1 | |
| b)Tứ giác ABCD có ∠ABD + ∠ACD = 1800
Nên ∠BAC + ∠BDC = 1800 |
1 | |
| c)M là trung điểm của đường chéo BC của hình bình hành BHCD nên M cũng là trung điểm của HD do đó H, M , D thẳng hàng | 0,5 | |
| d) OM là đường trung bình của ΔAHD nên OM = 1/2 AH | 0,5 |
