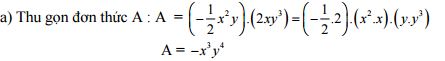Dưới đây là đề thi kiểm tra đánh giá chất lượng cuối năm học lớp 7 môn Toán được Phòng GD & ĐT Tam Đảo tổ chức thi…Cho tam giác ABC cân tại A, H là trung điểm của BC. Chứng minh: ΔAHB = ΔAHC.
Phần I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Chọn câu trả lời đúng nhất trong các câu sau:
Câu 1. Cho ΔABC có AB = 7 cm, AC = 5 cm, BC = 9 cm. So sánh nào sao đây là đúng?
A. ∠A> ∠B> ∠C
B. ∠B> ∠A> ∠C
C. ∠A> ∠C> ∠B
D. ∠C> ∠B> ∠A
Câu 2. Đa thức 5x2y2 – 10y2 có bậc là:
A. 1 B. 2 C. 3 D. 4
Câu 3. ΔABC cân tại A có B = 50o. Số đo của là:
A. 80o B. 50o C. 70o D. 60o
Câu 4. Đa thức 3x + 15 có nghiệm là:
A. – 3 B. – 5 C. 3 D. 5
Câu 5. Biểu thức nào sau đây là đơn thức?
Câu 6. Bộ ba độ dài đoạn thẳng nào sau đây không phải là ba cạnh của một tam giác?
A. 2 cm; 3 cm; 4 cm B. 12 cm; 14 cm; 16 cm
C. 9 cm; 12 cm; 22 cm D. 7 cm; 8 cm; 9 cm
Phần II. TỰ LUẬN (7,0 điểm)
Câu 7 (2,0 điểm). Cho đơn thức
a) Thu gọn đơn thức A.
b) Xác định phần hệ số, phần biến, bậc của đơn thức.
c) Tính giá trị của A tại x = 1 và y = – 1.
Câu 8 (2,0 điểm). Cho hai đa thức sau:
P(x) = – 3x2 + 5 – 4x4 + 2x – 5x3
Advertisements (Quảng cáo)
và Q(x) = 2x4 + 6x – 7x2 + 7x3 – 9
a) Hãy sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm dần của biến.
b) Tính P(x) + Q(x) và P(x) – Q(x).
Câu 9 (3,0 điểm). Cho tam giác ABC cân tại A, H là trung điểm của BC.
a) Chứng minh: ΔAHB = ΔAHC.
b) Vẽ HE⊥ AB; HF ⊥AC (E ∈ AB; F ∈ AC). Chứng minh HE = HF.
c) Biết số đo ∠BAH = 40o. Tính số đo ∠AHE.
d) Giả sử AB = 5 cm, BC = 6 cm. Tính AH.
Đáp án
PHẦN I. Trắc nghiệm khánh quan (3,0 điểm).
Học sinh chọn đúng mỗi câu được 0,5 điểm
| Câu | 1 | 2 | 3 | 4 | 5 | 6 |
| Đáp án | C | D | A | B | B | C |
Phần II. Tự luận (7 điểm)
Câu 7:
Advertisements (Quảng cáo)
b) Xác định phần hệ số, phần biến, bậc của đơn thức.
Phần hệ số: – 1
Phần biến: x3y4
Bậc của đơn thức: 7
c) Tính giá trị của A tại x = 1 và y = – 1
A = – (1)3(-1)4 = -1.1 = -1
Câu 8:
a) P(x) = – 4x4 – 5x3 – 3x2 + 2x + 5
Q(x) = 2x4 + 7x3 – 7x2 + 6x – 9
b)
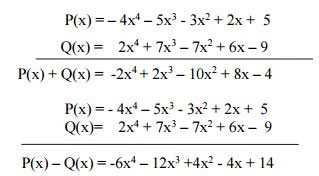
Câu 9:
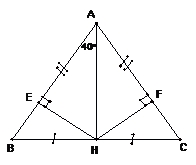
a) Chứng minh ΔAHB = ΔAHC
Xét ΔHAB và ΔHAC có
AB = AC (Vì ABC cân tại A)
∠B = ∠C (Vì ABC cân tại A)
HB = HC (Vì H là trung điểm của BC)
Vậy ΔHAB = ΔHAC (c – g – c)
b) Xét ΔBEH và ΔCFH có:
HB = HC (Vì H là trung điểm của BC)
∠B = ∠C (Vì ΔABC cân tại A)
∠BEH = ∠CFH = 90o (gt)
Vậy ΔBEH = ΔCFH (cạnh huyền – góc nhọn)
=> HE = HF
c) Biết số đo ∠BAH= 40o. Tính số đo ∠AHE = ?
Xét ΔAHE vuông tại E có: ∠BAH + ∠AHE = 90o.
40o + ∠AHE = 90o => ∠AHE = 90o – 40o = 50o
d)
Ta có ABC cân tại A có AH là đường trung tuyến nên AH cũng là đường cao. Vậy AHB vuông tại H.
Có: BH = HC = BC/2 = 6/2 = 3 cm
Áp dụng Pytago vào ΔAHB ta có:
AH2 + BH2 = AB2 => AH2 + 32 = 52
=> AH2 = 25 – 9 = 16 => AH = 4cm