Trường THCS Minh Khai Hà Nội đã tổ chức thi học kì 1 lớp 7 môn Toán năm học 2018 – 2019, trong đó bài hình có yêu cầu Chứng minh EF ⊥ AC.
TRƯỜNG THCS MINH KHAI ĐỀ KIỂM TRA HỌC KÌ I
MÔN TOÁN 7
Năm học 2018 – 2019
Thời gian làm bài: 90 phút
I. Trắc nghiệm (2 đ). Ghi vào bài làm chữ cái in hoa đứng trước câu trả lời đúng:
1. Cho hàm số y = f(x) – 2x + 1. Tính f(-1), ta được
A. 1 B. 3 C. 2 D. (-1)
2. Kết quả phép tính (-3)5 : (-3)3 bằng
Advertisements (Quảng cáo)
A. (-9) B. 1 C. 9 D. 27
3. Cho ∆HIK = ∆EPQ biết H = 900, P = 600. Số đo của góc K bằng
A. 600 B. 300 C. 900 D. 700
4. Cho ∆ABC và ∆DEF có B = E, AB = DE. Cần bổ sung thêm điều kiện nào dưới đây để ∆ABC = ∆DEF
A. C = F B. BC = EF C. AC = EF D. AC = DF
II. Tự luận
Advertisements (Quảng cáo)
1. (1,5đ) Thực hiện phép tính
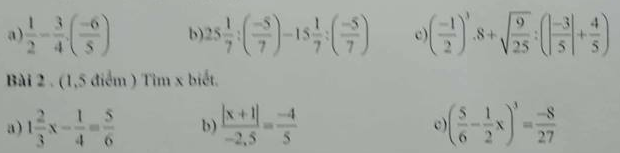
3. (1,5đ). Trong phong trào kế hoạch nhỏ đợt I, ba lớp 7 thu nhặt được 254 kg giấy vụn. Lớp 7A có 40 học sinh, lớp 7B có 42 học sinh, lớp 7C có 45 học sinh. Hỏi mỗi lớp thu gom được bao nhiêu kg giấy vụn, biết rằng số giấy vụn của mỗi lớp tỉ lệ với số học sinh.
4. (3đ) Cho ∆ABC vuông tại A, AB < AC. Vẽ AD vuông góc với BC (D thuộc BC). Trên tia đối của tia DA lấy điểm E sao cho AD = DE.
a)Chứng minh ∆ACD = ∆ECD
b) Chứng minh AB = BE
c) Trên đoạn DC lấy điểm F sao cho BD = DF. Chứng minh EF ⊥ AC
d) Gọi I là giao điểm của EF và AC. Trên CE lấy điểm K sao cho CK = CI. Chứng minh ba điểm A, F, K thẳng hàng
5. (0,5đ) Cho ba số x, y, z khác 0 và x + y + z ≠ 0 thỏa mãn điều kiện:
(y + z – 2x)/x = (z + x – 2y)/y = (x + y – 2z)/z. Hãy chứng tỏ A = [1 + x/y][1 + y/z][1 + z/x] là một số tự nhiên.