Định lí Pytago – chương 2: Giải bài 53, 54, 55, 56, 57 trang 131; 58 trang 132; bài 59, 60, 61, 62 trang 133 SGK Toán 7 tập 1
53. Tính
![bai 53 hinh 127]](https://dethikiemtra.com/wp-content/uploads/2015/11/bai-53-hinh-127.jpg)
Hình a)
Áp dụng ĐL Pytago, Ta có:
x2=122+52=144+25=169
=> x2 = 132 => x=13.
Hình b) ta có:
x2 = 12 + 22 = 1+4=5
x = √5
Hình c)
Theo ĐL pytago:
292 = 212+ x2
nên x2 =292 -212
= 841 – 441 = 400= 202
=>x = 20
Hình d)
x2=( √7)2 + 32= 7+9 =16= 42
x = 4.
54. Đoạn lên dốc từ C đến A dài 8.5cm, đô dài CB bằng 7,5cm.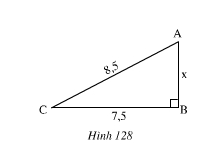
Tính chiều cao AB.
Theo địnhlípytago, ta có:
AB2 + BC2 = AC2
nên AB2 = AC2 – BC2
= 8,52 – 7,52
= 72,5-56,5=16
Vậy AB= 4
Bài 55 trang 131.Tính chiều cao của bức tường(h.129) biết rằng chiều cao của thang là 4m và chân thang cách tường 1m.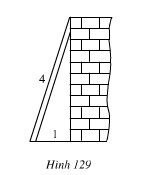
Theo đL pytago, ta có:
AC2+ BC2 = AB2
nên AC2 = AB2+BC2
Suy ra LAD = √15 ≈ 3.87
Luyện tập 1:
Advertisements (Quảng cáo)
Bài 56 Toán 7 tập 1. Tam giác nào là Δvuông trong các Δcó độ dài ba cạnh như sau:
a) 9cm,15cm,12cm.
b) 5dm,13dm,12cm.
c)7m,7m,10m.
Đáp án: a) Ta có 92 = 81,152 = 225, 122 =144.
mà 225=81+144
hay 152=92+122.
Nên Δ có độ dài ba cạnh 9cm,15cm,12cm là Δ vuông.
b) Ta có 52=25,132=169,122=144.
Mà 169=25+144 nên Δ có độ dài ba cạnh 5dm, 13dm,12dm là Δvuông
c) Ta có 72=49, 102=100
vậy 72+ 72 ≠102
72+102 ≠72
Nên Δ có độ dài 3 canh là 7dm,7dm,10dm không phải là Δvuông.
Bài 57. Cho bài toán “ΔABC có AB = 8cm, AB=17cm, AC =15cm có phải là Δvuông không?” Bạn Tâm giải thích như sau:
AB2+AC2 = 82+172 = 64+289
BC2=152=225
Do 352 ≠ 225 nên AB2+AC2 ≠BC2.
VậyΔABC không phải là Δvuông?
Lời giải trên đúng hay sai? nếu sai hai sửa lại cho đúng.
HD. Lời giải của bạn Tâm sai, sửa lại như sau:
Advertisements (Quảng cáo)
Ta có AB2+BC2=82+152=64+225=289
và AC2=172=289
Do đó AC2=BC2+AB2.
Vậy ΔABC là Δvuông.
Bài 58. Đố: Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ vướng vào trần nhà không?
 Gọi d là đường chéo của tủ, h là chiều cao của nhà. h= 21dm.
Gọi d là đường chéo của tủ, h là chiều cao của nhà. h= 21dm.
Ta có d2=202+42=400+16=416.
suy ra d= √416 (1)
Và h2=212=441, suy ra h= √441 (2)
So sánh (1) và (2) ta được d<h.
Như vậy anh Nam đẩy tủ đứng thẳng không bị vướng vào trần nhà.
Luyện tập 2:
59. Bạn Tâm muốn đóng cho một nẹp chéo AC để khung hình chữ nhật ABCD được vững hơn(h.134). Tính độ dài AC, Biết rằng AD=48 cm, CD=36 cm.
Bạn Tâm muốn đóng cho một nẹp chéo AC để khung hình chữ nhật ABCD được vững hơn(h.134). Tính độ dài AC, Biết rằng AD=48 cm, CD=36 cm.
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
60. Cho Δ nhọn ABC. Kẻ AH vuông góc với BC(H thuộc BC), cho biết AB=13,AH=12,HC=16 cm. Tính độ dài các cạnh của Δ ABC.

Vì AH ⊥ BC tại H nên ΔAHC vuông tại H
AC2= AH2+HC2= 122 +162 = 144 + 256 = 400.
⇒ AC = 20 (cm )
ΔAHB vuông tại H
BH2 = AB2 – AH2 =132 -122
= 169 – 144 = 25 ⇒ BH=5(cm)
Mà H ∈ BC Do đó BC= BH+HC= 5+16= 21(cm)
Bài 61 Toán 7 tập 1. Trên giấy ô vuông(Độ dài cạnh của ô vuông bằng 1), cho tam giác ABC như hình 125.)
Tính độ dài mỗi cạnh của ΔABC.

Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2 = AN2+NC2
= 9+16 = 25
nên AC = 5
BC2 = BK2 + KC2
= 32 + 52= 9+25=34
BC = √34
Bài 62. Đố: Người ta buộc con Cún bằng sợi dây có một đầu buộc tại điểm O làm cho con Cún cách điểm O nhiều nhất là 9m(h.136). Con cún có thể tới các vị trí A,B,C,D để canh giữ mảnh vườn hình chữ nhật ABCD hay không?(Các kích thước như trên hĩnh vẽ).
Ta có:
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C.






