Bài tập 33,34,35, 36,37,38, 39,40,41, 42 trang 123, 124 Toán 7 tập 1: Góc cạnh góc

Bài 5: Trường hợp bằng nhau thứ 3 của tam giác góc – cạnh -góc. (G.CG): Giải bài 33, 34, 35, 36,37 trang 123; Bài 38, 39, 40, 41, 42 trang 124 SGK Toán 7 tập 1. 

Bài 33. Vẽ ΔABC biết AC=2cm, ∠A = 90⁰,∠C = 60⁰

Cách vẽ:

– Vẽ đoạn AC=2cm,

– Trên cùng một nửa mặt phẳng bờ AC vẽ tia Ax và Cy sao cho ∠CAx = 90⁰, ∠ACy = 60⁰ 

Hai tia cắt nhau ở B. tạo thành ΔABC cần vẽ.

---

Bài 34. Trên mỗi hình 98,99 có Δnào bằng nhau? Vì sao?

• Xem hình 98

∆ABC và ∆ABD có:

∠CAB = ∠DAB(gt)

AB là cạnh chung.

∠CBA = ∠DBA (gt)

Nên ∆ABC=∆ABD(g.c.g)

• Xem hình 99.

Ta có:

∠ABC + ∠ABD =180⁰ (Hai góc kề bù).

∠ACB + ∠ACE =180⁰

Mà ∠ABC = ∠ACB(gt)

Nên ∠ABD = ∠ACE

* ∆ABD và ∆ACE có:

∠ABD = ∠ACE (cmt)

BD=EC(gt)

∠ADB = ∠AEC (gt)

Nên ∆ABD=∆ACE(g.c.g)

* ∆ADC và ∆AEB có:

∠ADC =  ∠AEB (gt)

∠ACD =  ∠ABE (gt)

Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB

Nên ∆ADC=∆AEB(g.c.g)

---

Bài 35 trang 123 Cho ∠xOy khác ∠bẹt, Ot là tia phân giác của góc đó. Qua H thuộc tia Ot , kẻ  đường ⊥ Ot, nó cắt Ox và Oy  theo thứ tự  A và B.

a) Chứng minh rằng OA=OB.

b ) Lấy điểm C thuộc tia Ot, chứng minh rằng CA=CB và
∠OAC  = ∠OBC

Đáp án: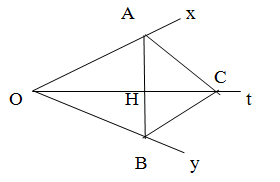

a) ∆AOH và  ∆BOH có:

∠AOH = ∠BOH (gt)

OH là cạnh chung

∠AHO = ∠OHB (=90⁰)

∆AOH =∆BOH( g.c.g)

Vậy OA=OB.

b)  ∆AOC và ∆BOC có:

OA = OB(cmt)

∠AOC = ∠BOC(gt)

OC cạnh chung.

Nên  ∆AOC= ∆BOC(c.g.c)

Suy ra: CA=CB(cạnh tương ứng)

∠OAC = ∠OAB( góc tương ứng).

---

Luyện tập 1 trang 123, 124

36. Trên hình 100 ta có OA=OB, ∠OAC =∠OBD.

Chứng minh rằng AC=BD.

Xét ∆OAC  và ∆OBD, có:

∠OAC =∠OBD(gt)

OA=OB(gt)

∠O  chung.

Nên ∆OAC=∆OBD(g.c.g)

Suy ra: AC = BD ( hai cạnh tương ứng )

---

37. Trên mỗi hình 101,102,103 có Δnào bằng nhau? Vì sao?

Tính các góc còn lại trên mỗi hình trên ta được:

∠A=60⁰, ∠H = 70⁰, ∠E = 40⁰ ,∠L =70⁰,

∠ RNQ =80⁰, ∠RNP= 80⁰

Hình 101: Ta được:   ∆ABC = ∆FDE(g. c.g)

Vì ∠B = ∠D = 80⁰ ( gt )

BC=DE

∠C = ∠E = 40⁰

Hình 102: ∆GHI không bằng ∆MKL

vì có GI = ML, ∠G = ∠M nhưng ∠I và ∠L không bằng nhau

Hình 103:  ∆NQR= ∆RPN(g.c .g)

Vì ∠RNQ = ∠RNP (=80⁰)

NR là cạnh chung.

∠NRP = ∠RNP (40⁰)

---

Bài 38.Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng minh rằng

AB=CD, AC=BD.

Vẽ đoạn thẳng AD.

∆ADB và ∆DAC có:

∠A₁ = ∠D₁ (so le trong AB//CD)

AD là cạnh chung.

∠A₂ = ∠D₂(So le trong, AC//BD)

Do đó ∆ADB=∆DAC(g.c .g)

Suy ra: AB=CD, BD=AC

---

Bài 39 trang 124 Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau? Vì sao?

Hình 105. ∆ABHvà ∆ACH có:

BH=CH(gt)

∠AHB = ∠AHC (∠vuông)

AH là cạnh chung.

vậy ∆ABH=∆ACH(c.g.c)

Hình 106. ∆DKE và ∆DKF có:
∠EDK = ∠FDK(gt)

DK là cạnh chung.
∠DKE = ∠DKF(∠vuông)

Vậy ∆DKE=∆DKF(g.c.g)

Hình 107. Ta có:

∠BAD = ∠CAD (gt)

AD chung

∆ABD=∆ACD(Cạnh huyền∠nhọn).

Hình 108. Δ ABD = Δ ACD (Cạnh huyền ∠nhọn)

⇒ AB = AC, DB = DC

Δ DBE = Δ DCH (g.c.g)

∆ABH=ACE (g.c.g)

---

40. Cho ΔABC(AB≠AC), tia Ax đi qua trung điểm M của BC.

Kẻ BE và CF ⊥ với Ax(E  ∈ Ax, F∈Ax ). So sánh độ dài BE và CF/

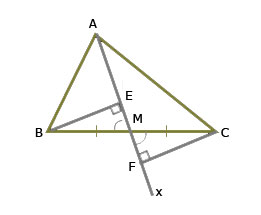
Hai Δ vuông BME, CMF có:

BM=MC(gt)

∠BME = ∠CMF(đối đỉnh)

Nên ∆BME=∆CMF(cạnh huyền- ∠nhọn).

Suy ra BE=CF. (2 cạnh tương ứng).

---

41. Cho ΔABC, cac tia phân giác của các ∠B và C cắt nhau ở I. Vẽ ID ⊥AB(D nằm trên AB), IE ⊥ BC (E thuộc BC ), IF ⊥ với AC(F thuộc AC)

CMR: ID=IE=IF.

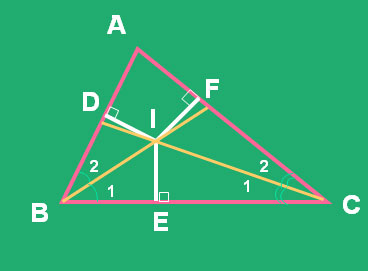
Hai Δvuông BID và BIE có:

BI là cạnh chung

∠B₁ = ∠B₂(do BI là tia phân giác ∠B)

nên ∆BID=∆BIE. (cạnh huyền – ∠nhọn)

Suy ra ID=IE (2 cạnh tương ứng) (1)

Tương tự:

CI là cạnh chung

∠C₁ = ∠C₂(do CI là tia phân giác ∠C)

∆CIE=CIF(cạnh huyền ∠nhọn).

Suy ra: IE =IF (2 cạnh tương ứng) (2)

Từ (1)(2) suy ra: ID=IE=IF.

---

 42. Cho ΔABC có ∠A= 90⁰, kẻ AH ⊥ BC(H∈BC). C ác ΔAHC và BAC có AC là cạnh chung,  ∠C chung, ∠AHC = ∠BAC =90⁰, nhưng hai Δkhông bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận  ∆AHC= ∆BAC?

ΔAHC và BAC có:

AC là cạnh chung

∠C  chung.

∠AHC = ∠BAC=90⁰,    Nhưng hai tam giác  không bằng nhau vì  ∠AHC  không phải là ∠kề với AC.