Bài 43, 44, 45 trang 125 SGK Toán lớp 7 tập 1: Luyện tập về ba trường hợp bằng nhau của tam giác

Đáp án và Giải bài 43, 44, 45 trang 125 SGK Toán 7 tập 1: Luyện tập về ba trường hợp bằng nhau của tam giác – Chương 2 hình học lớp 7.

Kiến thức:

– Tiếp tục củng cố  về ba trường hợp bằng nhau của tam giác c .c .c ; c.g.c và g.c.g

Kỹ năng:

– Nhận biết hai tam giác bằng nhau theo trường hợp bằng nhau góc – cạnh – góc ; Rèn kỹ năng vẽ hình và trình bày bài toán chứng minh.

– Rèn kỹ năng chứng minh hai tam giác bằng nhau, từ đó suy ra các cặp cạnh tương ứng bằng nhau và các cặp góc tương ứng bằng nhau; Rèn kỹ năng vẽ hình và chứng minh bài toán hình học.

Bài trước: Giải bài 33,34,35, 36,37,38, 39,40,41, 42 trang 123,124 SGK Toán 7 tập 1: Góc cạnh góc (Giải chi tiết)

Bài 43. Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA<OB.

Lấy các điểm C,D thuộc tia Oy sao cho OC=OA, OD=OB. Gọi E là giao điểm của AD và BC.

Chứng minh rằng:

a) AD=BC;

b) ∆EAB=∆ECD;

c )OE là tia phân giác của xOy.

Lời giải chi tiết:

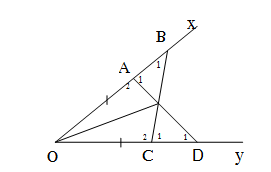
a) ∆OAD và ∆OCB có: OA= OC(gt)

∠O chung

OB = OD (gt)

OAD = OCB (c.g.c)  AD = BC

Nên ∆OAD=∆OCB(c.g.c)

suy ra AD=BC.

b)

Ta có  ∠A₁ = 180⁰ – ∠A₂

∠C₁ = 180⁰ – ∠C₂

mµ ∠A₂ = ∠C₂ do ΔOAD = ΔOCB (c/m trên)

⇒ ∠A₁ = ∠C₁

Ta có OB = OA + AB

OD = OC + CD mà OB = OD, OA = OC ⇒ AB = CD

Xét ΔEAB = ΔECD có:

∠A₁ = ∠C₁  (c/m trên)

AB = CD (c/m trên)

∠B₁ = ∠D₁ (ΔOCB = ΔOAD)

⇒ ΔEAB = ΔECD (g.c.g)

c) Xét ΔOBE và ΔODE có:

OB = OD (GT)

OE chung

AE = CE (ΔAEB = ΔCED)  ⇒ΔOBE = ΔODE (c.c.c)

⇒ ∠AOE = ∠COE  ⇒ OE là phân giác của góc ∠xOy.

---

Bài 44 trang 125. 

Cho tam giác ABC có ∠B = ∠C. Tia phân giác của góc A cắt BC tại D.

Chứng minh rằng.

a)  ∆ADB=∆ADC.

b) AB=AC.

Đáp án và hướng dẫn giải bài 44: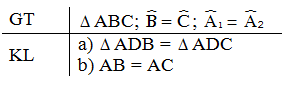a) Ta có:

Xét ΔADB và ΔADC có: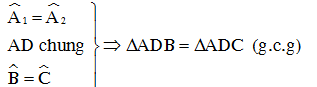

b) ∆ADB=∆ADC(chứng minh câu a)

Suy ra AB=AC .

---

Bài 45 Toán 7 tập 1.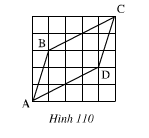

Đố:  Cho 4 đoạn thẳng AB,BC,CD,DA trên giấy kẻ ô vuông như ở hinh 110. Hãy lập luận để giải thích:

a) AB=CD, BC=AD;

b) AB//CD.

Lời giải chi tiết:

∆AHB và ∆CKD có:

HB= KD.
∠AHB=∠CKD

AH=CK

Nên ∆ AHB = ∆  CKD(c.g.c)

suy ra AB=CD.

tương tự ∆ CEB = ∆ AFD(c.g.c)

suy ra BC=AD.

b) ∆ABD và ∆CDB  có:

AB=CD(câu a)

BC=AD(câu a)

BD chung.

Do đó ∆ABD=∆CDB(c.c .c)

Suy ra  ∠ABD = ∠CDB

Vậy AB // CD( hai góc so le trong bằng nhau) .