Chia sẻ đề thi Toán học kì 1 lớp 8: Tìm giá trị nguyên của x để A có giá trị nguyên?

Bài 1 (2đ)Phân tích các đa thức sau thành nhân tử:

a)\(2{x^3} – 50x\)

b)\({x^2} – 6x + 9 – 4{y^2}\)

c)\({x^2} – 7x + 10\)

Bài 2 (1,5đ)

a.Làm tính chia: \(\left( {12{x^6}{y^4} + 9{x^5}{y^3} – 15{x^2}{y^3}} \right):3{x^2}{y^3}\)

b. Rút gọn biểu thức: \(\left( {{x^2} – 2} \right)\left( {1 – x} \right) + \left( {x + 3} \right)\left( {{x^2} – 3x + 9} \right)\)

Bài 3 (2,5đ)Cho biểu thức: \(A = \dfrac{5}{{x + 3}} – \dfrac{2}{{3 – x}} – \dfrac{{3{x^2} – 2x – 9}}{{{x^2} – 9}}\) (với \(x \ne  \pm 3\))

a)Rút gọn biểu thức \(A\).

b)Tính giá trị của \(A\) khi \(\left| {x – 2} \right| = 1\)

c)Tìm giá trị nguyên của \(x\) để\(A\) có giá trị nguyên.

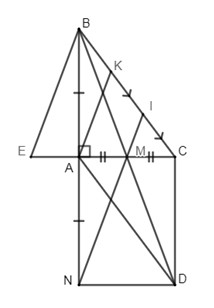
Bài 4 (3,5đ)Cho \(\Delta ABC\)vuông tại \(A\), gọi \(M\) là trung điểm của \(AC\). Gọi \(D\) là điểm đối xứng với \(B\)  qua \(M\).

a)Chứng minh tứ giác \(ABC{\rm{D}}\) là hình bình hành.

b)Gọi \(N\) là điểm đối xứng với \(B\)  qua \(A\). Chứng minh tứ giác \(AC{\rm{D}}N\) là hình chữ nhật.

c)Kéo dài \(MN\) cắt \(BC\) tại \(I\). Vẽ đường thẳng qua \(A\) song song với \(MN\) cắt \(BC\) ở\(K\). Chứng minh: \(KC = 2BK\)

d)Qua \(B\) kẻ đường thẳng song song với \(MN\) cắt \(AC\) kéo dài tại \(E\) . Tam giác \(ABC\) cần có thêm điều kiện gì để tứ giác \(EBMN\) là hình vuông.

Bài 5 (0,5đ)Cho \(a\) thỏa mãn: \({a^2} – 5a + 2 = 0\). Tính giá trị của biểu thức:\(P = {a^5} – {a^4} – 18{a^3} + 9{a^2} – 5a + 2017 + \left( {{a^4} – 40{a^2} + 4} \right):{a^2}\)

Bài 1. \(\begin{array}{l}a)\,\,2{x^3} – 50x\,\\{\rm{ = }}\,{\rm{2}}x\left( {{x^2} – 25} \right)\\ = 2x\left( {x – 5} \right)\left( {x + 5} \right)\end{array}\)

\(\begin{array}{l}b)\,\,{x^2} – 6x + 9 – 4{y^2}\\ = {\left( {x – 3} \right)^2} – 4{y^2}\\ = \left( {x – 3 + 2y} \right)\left( {x – 3 – 2y} \right)\end{array}\)

\(\begin{array}{l}c)\,{x^2} – 7x + 10\\ = {x^2} – 5x{\rm{ }} – 2x + 10\\ = \left( {{x^2} – 5{\rm{x}}} \right) – \left( {2x – 10} \right)\\ = x\left( {x – 5} \right) – 2\left( {x – 5} \right)\\ = \left( {x – 5} \right)\left( {x – 2} \right)\end{array}\)

Bài 2: \(\begin{array}{l}a)\,\,\left( {12{x^6}{y^4} + 9{x^5}{y^3} – 15{x^2}{y^3}} \right):3{x^2}{y^3}\\ = \left( {12{{\rm{x}}^6}{y^4}:3{{\rm{x}}^2}{y^3}} \right) + \left( {9{x^5}{y^3}:3{x^2}{y^3}} \right) – \left( {15{x^2}{y^3}:3{x^2}{y^3}} \right)\\ = 4{x^4}y + 3{x^3} – 5\end{array}\)\(\begin{array}{l}b)\,\,\left( {{x^2} – 2} \right)\left( {1 – x} \right) + \left( {x + 3} \right)\left( {{x^2} – 3x + 9} \right)\\ = {x^2} – {x^3} – 2 + 2x + {x^3} – 3{x^2} + 9x + 3{x^2} – 9x + 27\\ = {x^2} + 2x + 25\end{array}\)

Bài 3 \(\begin{array}{l}a)\,\,A = \dfrac{5}{{x + 3}} – \dfrac{2}{{3 – x}} – \dfrac{{3{x^2} – 2x – 9}}{{{x^2} – 9}}\,\,\left( {x \ne  \pm 3} \right)\\ = \dfrac{5}{{x + 3}} + \dfrac{2}{{x – 3}} – \dfrac{{3{x^2} – 2x – 9}}{{\left( {x – 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{5\left( {x – 3} \right) + 2\left( {x + 3} \right) – 3{{\rm{x}}^2} + 2x{\rm{ + }}9}}{{\left( {x + 3} \right)\left( {x – 3} \right)}}\\ = \dfrac{{5x – 15 + 2x + 6 – 3{x^2} + 2x\,{\rm{ + }}\,9}}{{\left( {x + 3} \right)\left( {x – 3} \right)}}\\ = \dfrac{{ – 3{x^2} + 9x}}{{\left( {x + 3} \right)\left( {x – 3} \right)}}\\ = \dfrac{{ – 3x\left( {x – 3} \right)}}{{\left( {x + 3} \right)\left( {x – 3} \right)}} = \dfrac{{ – 3x}}{{x + 3}}.\end{array}\)

\(b)\,\,\left| {x – 2} \right| = 1 \Rightarrow \left[ \begin{array}{l}x – 2 = 1\\x – 2 =  – 1\end{array} \right. \)

\(\Rightarrow \left[ \begin{array}{l}x = 3\left( {ktm} \right)\\x = 1\left( {tm} \right)\end{array} \right.\)

Với \(x = 1\) thay vào A ta có: \(A = \dfrac{{ – 3.1}}{{1 + 3}} = \dfrac{{ – 3}}{4}\).

c) Ta có: \(A = \dfrac{{ – 3x}}{{x + 3}} =  – 3 + \dfrac{9}{{x + 3}}\), để\(A\) nguyên \( \Leftrightarrow \left( {x + 3} \right) \in U\left( 9 \right) = \left\{ { \pm 1;\; \pm 3;\; \pm 9} \right\}\)

Vậy với \(x \in \left\{ { – 2; – 4;\;0; – 6;\;6; – 12} \right\}\) thì \(A\) nguyên.

Bài 4:

a) Ta có: Vì \(D\)  và \(B\) đối xứng với nhau qua \(M\) (gt)\( \Rightarrow M{\rm{D}} = MB\)(tính chất hai điểm đối xứng với nhau qua 1đ)

Xét tứ giác \(ABC{\rm{D}}\) ta có: \(\left\{ \begin{array}{l}MC = MA\left( {gt} \right)\\M{\rm{D}} = MB\left( {cmt} \right)\end{array} \right.\)

\( \Rightarrow \) Tứ giác \(ABC{\rm{D}}\) là hình bình hành (dhnb)

b)Vì \(N\) đối xứng với \(B\)  qua \(A\) (gt)

\( \Rightarrow NA = AB\)(tính chất)

Lại có \(ABC{\rm{D}}\) là hình bình hành (cmt)

\( \Rightarrow \left\{ \begin{array}{l}DC = AB\\DC//AB\end{array} \right.\)(tính chất) \( \Rightarrow \left\{ \begin{array}{l}DC = AN\\DC//AN\end{array} \right.\)

\( \Rightarrow AN{\rm{D}}C\) là hình bình hành (dhnb)

      Mặt khác, \(\angle CAB = {90^0}\left( {gt} \right) \Rightarrow \angle CAN = {90^0}\)

\( \Rightarrow \)hình bình hành \(AN{\rm{D}}C\) là hình chữ nhật (dhnb) (đpcm)

c)Xét \(\Delta BNI\) có: \(AK//NI\) (do \(AK//MN\) )

\(NA = AB\left( {gt} \right)\)

\( \Rightarrow \)\(AK\) là đường trung bình của \(\Delta BNI\)(định lý)

\( \Rightarrow KI = KB\) (tính chất)

Xét \(\Delta CAK\) có: \(MI//AK\) (do \(AK//NI\))

\(MA = MC\) (gt)

\( \Rightarrow \)\(MI\) là đường trung bình của \(\Delta ACK\) (dhnb)

\( \Rightarrow IK = CI\) (tính chất)

Mà \(KC = CI + IK \Rightarrow KC = 2KI = 2KB\) (do \(KI = KB\))

d)Vì \(BE//MN\left( {gt} \right) \Rightarrow BE//IM \Rightarrow \) Tứ giác \(BEMI\) là hình thang (dấu hiệu nhận biết hình thang)

Lại có: K là trung điểm của BI (cmt) và \(AK//MI\left( {cmt} \right) \Rightarrow A\)là trung điểm của EM (trong hình thang, nếu một đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì đi qua trung điểm của cạnh bên thứ hai)

Xét tứ giác \(BENM\) có hai đường chéo BN và EM cắt nhau tại trung điểm A của mỗi đường.

\( \Rightarrow BENM\)là hình bình hành (dhnb)

Mà \(BN \bot EM\left( {gt} \right) \Rightarrow \) hình bình hành BENM là hình thoi (dhnb)

Để hình thoi BENM là hình vuông khi và chỉ khi \(AB = AM \Leftrightarrow AB = \dfrac{1}{2}AC\).

Bài 5: \(\begin{array}{l}P = {a^5} – {a^4} – 18{a^3} + 9{a^2} – 5a + 2017 + \left( {{a^4} – 40{a^2} + 4} \right):{a^2}\\\;\;\; = \left( {{a^5} – 5{a^4} + 2{a^3}} \right) + \left( {4{a^4} – 20{a^3} + 8{a^2}} \right) + \left( {{a^2} – 5a + 2} \right) + 2015 + \dfrac{{{a^4} – 40{a^2} + 4}}{{{a^2}}}\\\;\;\; = {a^3}\left( {{a^2} – 5a + 2} \right) + 4{a^2}\left( {{a^2} – 5a + 2} \right) + 2015 + \dfrac{{{a^4} – 40{a^2} + 4}}{{{a^2}}}\\\;\;\; = 2015 + \dfrac{{{a^4} – 40{a^2} + 4}}{{{a^2}}}\\\;\;\; = \dfrac{{{a^4} + 1975{a^2} + 4}}{4}.\end{array}\)

Theo đề bài ta có: \({a^2} – 5a =  – 2 \Rightarrow {\left( {{a^2} – 5a} \right)^2} = 4 \Rightarrow {a^4} – 10{a^3} + 25{a^2} = 4\)

\(\begin{array}{l}P = \dfrac{{{a^4} + 1975{a^2} + 4}}{{{a^2}}}\\\;\;\; = \dfrac{{\left( {{a^4} – 10{{\rm{a}}^3} + 25{{\rm{a}}^2}} \right) + \left( {10{a^3} – 50{a^2} + 20a} \right) + \left( {4{a^2} – 20a + 8} \right) + 1996{a^2} – 4}}{{{a^2}}}\\\;\;\; = \dfrac{{4 + 10a\left( {{a^2} – 5a + 2} \right) + 4\left( {{a^2} – 5a + 2} \right) + 1996{a^2} – 4}}{{{a^2}}} = 1996\end{array}\)

Vậy \(P = 1996.\)