Đề kiểm tra 1 tiết Chương 1 – Tứ giác môn Hình lớp 8: Tứ giác OBEC là hình gì ? Tại sao ?

Bài 1. Cho hình thoi ABCD có O là giao điểm hai đường chéo. Gọi I là trung điểm cạnh BC và E là trung điểm đối xứng với O qua I.

a) Tứ giác OBEC là hình gì ? Tại sao ?

b)Chứng tỏ E đối xứng với A qua trung điểm J của đoạn OB.

Bài 2. Cho tam giác ABC vuông tại A (AB < AC). Gọi I là trung điểm của BC. Qua I vẽ \(IM \bot AB\) tại \(IN \bot AC\) tại N.

a)Chứng minh AMIN là hình chữ nhật.

b)Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.

c)Đường thẳng BN cắt DC tại K. Chứng minh \({{DK} \over {DC}} = {1 \over 3}.\)

Bài 1.

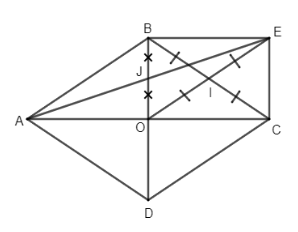
a) Ta có IB = IC (gt), IO = IE (tính chất đối xứng)

\( \Rightarrow OBEC\) là hình bình hành.

Lại có \(\widehat {BOC} = {90^ \circ }\) (tính chất hai đường chéo hình thoi).

Do đó OBEC là hình chữ nhật.

b) Ta có OC = OA (tính chất đường chéo hình thoi)

Mà OC = BE và \(OC\parallel BE\left( {cmt} \right)\) nên OA = BE và \(OA\parallel BE.\) Do đó ABEO là hình bình hành có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.

Chứng tỏ E đối xứng với A qua trung điểm J của đoạn OB.

Bài 2.

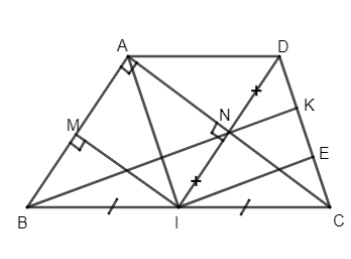
a) Tứ giác ANIM là hình chữ nhật (có ba góc vuông).

b) I là trung diểm của BC nên AI là đường trung tuyến của tam giác vuông ABC.

\( \Rightarrow AI = IC = {{BC} \over 2}.\)

Do đó \(\Delta AIC\) cân có IN là đường cao nên đồng thời là trung tuyến hay NA = NC, lại có NI = ND (tính chất đối xứng) \(\Rightarrow ADCI\) là hình thoi.

c) Kẻ qua I đường thẳng song song với BK cắt CD tại E. Ta có IE là đường trung bình của  \(\Delta BKC\)

\( \Rightarrow E\) là trung điểm của CK hay EK = EC   (1)

Mặt khác N là trung điểm của ID và \(NK\parallel IE\left( {IE\parallel BK} \right)\) nên NK là đường trung bình của \(\Delta DIE\)

\( \Rightarrow K\) là trung điểm của DE hay EK = DK   (2)

Từ (1) và (2) \( \Rightarrow {{DK} \over {DC}} = {1 \over 3}.\)