
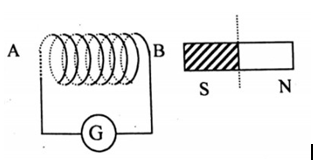
1. Có 1 nam châm và ống dây như hình vẽ, để tạo ra dòng điện cảm ứng, người ta dùng các cách nào?
2.Đường dây truyền tải điện có hiệu điện thế 15kV ở hai đầu nơi truyển tải, công suất cung cấp ở nơi truyền tải P = 3.106W. Dây dẫn tải điện cứ 1km thì có điện trở 0,2Ω, công suất hao phí do tỏa nhiệt trên đường dây Php = 160kW. Tính chiều dài tổng cộng l của dây dẫn
3.Đặt 1 vật sáng vuông góc với trục chính của thấu kính hội tụ có tiêu cự 15cm cách thấu kính d=30cm ta được ảnh gì và cách thấu kính bao nhiêu?
4.Một vật sáng AB cao 4cm đặt vuông góc với trục chính của 1 thấu kính hội tụ cách thấu kính 20cm, cho 1 ảnh thật cách vật 60cm. Hỏi ảnh của vật cao bao nhiêu
5.Đặt một vật sáng AB vuông góc với trục chính của thấu kính phân kỳ cách thấu kính 12cm. tiêu cự của thấu kính 6cm. tìm vị trí của ảnh.

1. : Để tạo ra dòng điện cảm ứng người ta dùng các cách sau: đưa cực nam châm lại gần hoặc đưa cực nam châm ra xa ống dây, quay nam châm xung quanh 1 trục thẳng đứng.
2. : Cường độ dòng điện qua dây \(I = \dfrac{P}{U} = \dfrac{{{{3.10}^6}}}{{15000}} = 200\,A\)
Công suất hao phí
\({P_{hp}} = {I^2}R \Rightarrow R = \dfrac {{{P_{hp}}} }{ {I{}^2}} = 4\Omega \)
Advertisements (Quảng cáo)
Điện trở dây dẫn \(R = 0,2.L = 4Ω.\)
Chiều dài đường dây là \(L = \dfrac{4}{{0,2}} = 20\,km\)
3. : Vật sáng đặt ngoài tiêu cự vậy qua thấu kính hội tụ cho một ảnh thật, ngược chiều với vật như hình vẽ:
Từ ∆ABO đồng dạng ∆A’B’O
\(\Rightarrow \dfrac {{A’B’} }{ {AB}} = \dfrac {{OA’} }{ {OA}}\) (1)
∆OIF đồng dạng ∆A’B’F
\(\Rightarrow \dfrac {{A’B’} }{ {OI}} = \dfrac {{F’A’} }{ {OF’}}\) (2)
Và OI = AB nên từ (1) và (2) suy ra:
Advertisements (Quảng cáo)
Từ (1) cho ta
\(\dfrac {{OA} }{ {OA’}} = \dfrac {{{ {OF}}} }{ {F’A’}}\)
\(\Leftrightarrow \dfrac {{OA} }{ {OA’}} = \dfrac {{OF’} }{ {OA’ – OF’}}\)
\(\Leftrightarrow \dfrac {d }{ {d’}} = \dfrac {f }{ {d’ – f}}\)
\(\dfrac{{30} }{ {d’}} = \dfrac{{15} }{{d’ – 15}}\) giải ra ta được \(d’ = 30cm.\)
Vậy ảnh thật cách thấu kính 30cm.
4. : Hình vẽ tương tự hình 3 ta có:
\(\dfrac {{A’B’} }{ {AB}} =\dfrac {{OA’} }{ {OA}} = \dfrac {{AA’ – OA} }{ {OA}} \)\(\;= \dfrac {{60 – 20} }{ {20}} = 2\)
\(\Rightarrow A’B’ = AB.2 = 4.2 =8cm\)
5. Vật sáng đặt trước thấu kính phân kỳ cho ảnh như hình vẽ:
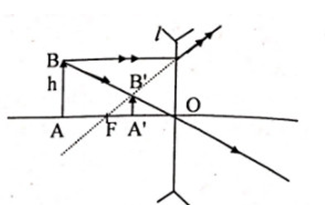
Từ hình, Từ ∆ABO đồng dạng ∆A’B’O
\(\Rightarrow \dfrac {{A’B’} }{ {AB}} = \dfrac {{OA’} }{ {OA}} = \dfrac {{d’} }{ d}\) (1)
∆F’A’B’ đồng dạng ∆F’OI
\(\Rightarrow \dfrac {{A’B’} }{ {OI}} =\dfrac {{F’A’} }{ {OF’}} = \dfrac {{f – d’} }{ f}\) (2)
Từ (1) và (2) suy ra:
\(\dfrac {d }{ {d’}} =\dfrac {f }{ {d’ – f}} = \dfrac {{12} }{ {d’}} = \dfrac {6 }{ {6d’}}\)
\(\Leftrightarrow d’ = 12 – 2d’ \Rightarrow d’ = 4cm\)






