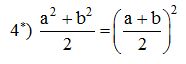Đề thi kiểm tra giữa học kì 2 môn Toán lớp 8 có đáp án gồm Đại Số và Hình Học của Phòng GD & ĐT Bình Giang năm học 2014- 2015. Thời gian làm bài 90 phút.
A. Phần Đại Số ( 45 phút)
1 . Giải các phương trình:
1) 3x -12 = 0
3) (x + 3) (2x – 4) = 0
2 . Cho a < b, hãy so sánh:
1) a + 2 và b + 2 2) a – 3 và b – 3
3) -3a và -3b 4) 2a + 1 và 2b – 1
3 . So sánh a và b nếu:
1) a + 5 > b + 5
3) 2 – a ≤ 2 – b
4 . Giải bài toán bằng cách lập phương trình:
Một canô xuôi dòng từ bến A đến bến B mất 3 giờ và ngược dòng từ bến B về bến A mất 4 giờ. Tính khoảng cách giữa hai bến A và B, biết vận tốc của dòng nước là 2,5 km/h.
Đáp án phần Đại Số
1. 1) 3x – 12 = 0 ⇔ 3x = 12 ⇔ x = 4 (0,75đ)
Vậy phương trình có tập nghiệm là S = {4} (0,25đ)
(0,5đ)
⇔ x = 6 Vậy phương trình có tập nghiệm là S = {6} (0,5đ)
3) (x + 3)(2x – 4) = 0 ⇔ x + 3 = 0 hoặc 2x – 4 = 0 ⇔ x = -3 hoặc 2x = 4 (0,5đ)
⇔ x = -3 hoặc x = 2. Vậy phương trình có tập nghiệm là S = {-3;2}
4) ĐKXĐ: x ≠ 2 ; x ≠ -2
0,5 đ
⇔ x – 2 + 2x + 4 = 8 ⇔ 3x + 2 = 8 ⇔ x = 2 (loại).
Vậy phương trình đã cho vô nghiệm
2. 1) Do a < b ⇒ a + 2 < b + 2
2) Do a < b ⇒ a + (-3) < b + (-3) ⇒ a – 3 < b – 3
Advertisements (Quảng cáo)
3) Do a < b ⇒ (-3) .a > (-3) .b ⇒ -3a > – 3b
4) Do a < b ⇒ 2a < 2b
⇒ 2a + 1 < 2b + 1
3.1) a + 5 > b + 5 ⇒ a + 5 + (-5) > b + 5 + (-5)
⇒ a > b. Vậy a > b. (0,25 đ)
⇒ a < b. Vậy a < b. (0,25 đ)
3) 2 – a ≤ 2 – b ⇒ 2 –a + (-2) ≤ 2 – b + (-2)
⇒ -a ≤ -b ⇒ a ≥ b . Vậy a ≥ b. (0,25 đ)
= ( a + b)² ⇒ 2a² + ab² = a² + 2ab + b² (0,25 đ)
⇒ a² – 2ab + b² = 0 ⇒ (a – b)² = 0 ⇒ a = b. Vậy a = b. (0,25 đ)
4.Gọi khoảng cách giữa hai bến A và B là x (km), điều kiện:
x > 0
Vận tốc canô đi từ A đến B là x/3 (km/h)
Vận tốc canô đi từ B về A là x/4 (km/h)
Do vận tốc của dòng nước là 2,5 km/h, vận tốc thực canô không đổi nên ta có PT:
0,25đ
Advertisements (Quảng cáo)
⇔ 4x – 30 = 3x + 30
⇔ x = 60 (Thỏa mãn điều kiện)
Vậy khoảng cách giữa hai bến A và B là 60 km.
B.Phần Hình Học ( 45 phút)
1. Cho tam giác ABC, lấy hai điểm M và N thứ tự thuộc hai cạnh AB và AC sao cho MN // BC, biết AM = 4cm, MB = 2cm, MN = 5cm, AC = 9cm. Tính các độ dài AN, BC.
2 . Không cần vẽ hình, hãy cho biết ΔABC đồng dạng với ΔMNK trong những trường hợp nào sau đây ? Vì sao ?
a) AB = 6cm, BC = 9cm, AC = 12cm và MN = 2cm, NK = 4mm, MK = 5mm;
b) AB = 4cm, BC = 5cm, AC = 6cm và MN = 8mm, NK = 10mm, MK = 12mm;
c) ∠A = 80º , ∠B = 60º và ∠M = 80º , ∠N = 62º
d) ∠A = 65º , ∠B = 70º và ∠M = 65º , ∠K = 45º
e) AB = 4cm, AC = 6cm, ∠A = 50º và MN = 2cm, MK = 3cm ∠M = 50º,;
f) AB = 3cm, AC = 6cm, ∠A = 50º và MN = 2cm, MK = 4cm, ∠N = 50º,;;
3 . Cho Δ ABC (∠A = 90º), các đường cao AK, BE, CF . Gọi H là trực tâm của ΔABC.
Chứng minh rằng:
1) Δ ABE đồngdạng với ΔACF;
2) ∠AEF = ∠ABC
3) H là giao điểm các đường phân giác của ΔKEF.
Đáp án phần hình học
1.
Vẽ hình 0,5 điểm
Ta có: AB = AM + MB = 4 + 2 = 6(cm)
Do MN // BC nên:
0,5 điểm
0,5đ
AN = 6cm, BC = 7,5cm
2.b) ΔABC đồng dạng với ΔMNK (c.c.c) (0,5đ)
0,5 điểm
d) Tính ∠C = 45º ⇒ ΔABC đồng dạng với ΔMNK (g.g) (0,5đ)
Vì ∠A = ∠M = 65º; ∠C = ∠K = 45º (0,5đ)
e) ΔABC đồng dạng với ΔMNK (c.g.c) (0,5đ)
0,5 điểm
3.
Vẽ hình đúng 0,5 điểm
1) Xét Δ ADE và Δ ACF có:
∠AEB = ∠AFC = 90º, góc BAC chung
⇒ Δ ABE đồng dạng với Δ ACF (g.g)
2) Theo a) Δ ABE đồng dạng với Δ ACF
Xét ΔAEF và ΔABC có:
Góc BAC chung 
⇒ ΔAEF đồng dạng với ΔABC (c.g.c)
⇒∠AEF = ∠ABC
3) Theo b) ∠AEF = ∠AB
C.CM tương tự ta có: ∠CEK = ∠ABC
Suy ra ∠AEF = ∠CEK, mà ∠ BEA = ∠BEC = 90º
⇒ ∠HEF = ∠HEK suy ra EH là tia phân giác của ΔKEF
Chứng minh tương tự ta có: FH, KH là các tia phân giác của ΔKEF
Vậy H là giao điểm các đường phân giác của ΔKEF.
