Bài 1 (1,5đ):Thực hiện các phép tính sau:
a) \(\dfrac{1}{2} – \dfrac{2}{3} + \dfrac{1}{6} \)
b) \( {5^9}:{5^7} – \sqrt {25} – \left| { – 5} \right|\)
Bài 2 (1,0đ):Tìm \(x\), biết:
\(a)\,\,x – \dfrac{7}{5} = – \dfrac{2}{5}\,\,\, b)\,\,\left| {x – 3} \right| + 5 = 2019\)
Bài 3 (1,5đ):
a) Cho hàm số \(y = f(x) = 2{x^2} – 3\). Tính: \(f(0)\,;\,\,\,f(2)\).
b) Vẽ đồ thị hàm số \(y = – 2x\).
Bài 4 (1,5đ):Ba lớp 7A, 7B, 7C tham gia đóng góp ủng hộ hội người khuyết tật với tổng số tiền là \(600\,\,000\) đồng. Tính số tiền mà mỗi lớp đóng góp, biết số tiền ủng hộ của ba lớp lần lượt tỉ lệ thuận với \(5\,;\,\,7\,;\,\,8\).
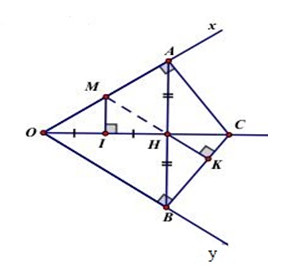
Bài 5 (4,0đ):Cho góc nhọn \(xOy\), trên tia \({\rm{O}}x\) lấy điểm \(A\), trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA = OB\). Gọi \(H\) là trung điểm của đoạn thẳng \(AB\).
a) Chứng minh: \(\Delta OAH = \Delta OBH\).
b) Từ \(A\) vẽ đường thẳng vuông góc với đường thẳng \(OA\), đường thẳng này cắt tia OH tại \(C\). Chứng minh: \(AC = BC\).
c) Gọi \(I\) là trung điểm của đoạn thẳng \(OH\), từ \(I\) vẽ đường thẳng vuông góc với cạnh \(OH\), đường thẳng này cắt tia \(OA\) tại \(M\). Chứng minh: \(MI\)//\(AB\).
d) Từ \(H\) vẽ đường thẳng vuông góc với cạnh \(BC\)tại \(K\). Chứng minh ba điểm \(M,\,\,H,\,\,K\) thẳng hàng.
Bài 6 (0,5đ).Tìm hai số hữu tỉ \(x\) và \(y\,\,(y \ne 0)\) biết rằng \(x + y = x.y = x:y\).
Bài 1: \(\begin{array}{l}a)\,\,\dfrac{1}{2} – \dfrac{2}{3} + \dfrac{1}{6}\,\, \\= \dfrac{3}{6} – \dfrac{4}{6} + \dfrac{1}{6}\,\, \\= \dfrac{{3 – 4 + 1}}{6}\, = \dfrac{0}{6} = 0\\b)\,\,{5^9}:{5^7} – \sqrt {25} – \left| { – 5} \right|\,\, \\= {5^{9 – 7}} – 5 – 5 = {5^2} – 5 – 5\\ = 25 – 5 – 5 = 20 – 5 = 15.\end{array}\)
Bài 2: \(\begin{array}{l}a)\,\,x – \dfrac{7}{5} = – \dfrac{2}{5}\,\\ \Leftrightarrow \,x = – \dfrac{2}{5} + \dfrac{7}{5}\,\,\\ \Leftrightarrow x = \dfrac{5}{5} = 1.\end{array}\)
\(\begin{array}{l}b)\,\,\left| {x – 3} \right| + 5 = 2019\\ \Leftrightarrow \,\left| {x – 3} \right| = 2019 – 5\\ \Leftrightarrow \,\left| {x – 3} \right| = 2014\\ \Leftrightarrow \left[ \begin{array}{l}x – 3 = 2014\\x – 3 = – 2014\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2014 + 3\\x = – 2014 + 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2017\\x = – 2011\end{array} \right.\end{array}\)
Bài 3: a) Ta có:
Advertisements (Quảng cáo)
\(\begin{array}{l}f(0) = {2.0^2} – 3 = 2.0 – 3 = 0 – 3 = – 3\\f(2) = {2.2^2} – 3 = 2.4 – 3 = 8 – 3 = 5\end{array}\)
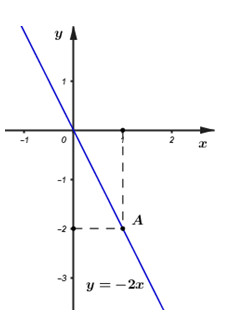
b) Vẽ đồ thị hàm số \(y = – 2x\)
Đồ thị hàm số \(y = – 2x\) là một đường thẳng đi qua gốc tọa độ \(O\).
Cho \(x = 1\)suy ra \(y = – 2.1 = – 2\). Khi đó ta có điểm \(A(1; – 2)\).
Đồ thị hàm số \(y = – 2x\) là đường thẳng \(OA\) (xem hình vẽ)
Bài 4: Gọi số tiền đóng góp được của ba lớp7A, 7B, 7C lần lượt là \(a,\,\,b,\,\,c\,\,(0\; < \;a,\,\,b,\,\,c\; < \;600\;000).\)
Theo đề bài số tiền đóng góp được của lớp 7A, 7B, 7C tỉ lệ với \(5,\,\,7,\,\,8\)nên \(\dfrac{a}{5} = \dfrac{b}{7} = \dfrac{c}{8}\)
Tổng số tiền đóng góp được của \(3\) lớp là \(600000\) đồng nên ta có \(a + b + c = 600000\).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\dfrac{a}{5} = \dfrac{b}{7} = \dfrac{c}{8} = \dfrac{{a + b + c}}{{5 + 7 + 8}} = \dfrac{{600000}}{{20}} = 30000\\ \Rightarrow a = 30000.5 = 150000\;\;\left( {tm} \right)\\\,\,\,\,\,\,\,b = 30000.7 = 210000\;\;\left( {tm} \right)\\\,\,\,\,\,\,\,c = 30000.8 = 240000\;\;\left( {tm} \right)\end{array}\)
Vậy lớp 7A góp được \(150000\) đồng, lớp 7B góp được \(210000\) đồng, lớp 7C góp được \(240000\) đồng.
Bài 5:
Advertisements (Quảng cáo)
|
GT |
Góc nhọn \(xOy\,;\,\,A \in Ox\,;\,\,B \in Oy\,;\,\,OA = OB\,;\,\,H\) là trung điểm của \(AB\). \(C \in \) tia \(OH\); \(AC \bot OA\); \(I\) là trung điểm của \(OH\) \(M \in \) tia \(OH\); \(MI \bot OC\); \(K \in BC\,;\,\,HK \bot BC\) |
|
KL |
a) \(\Delta OAH = \Delta OBH\). b)\(AC = BC\). c) \(MI\) // \(AB\).b)\(AC = BC\). d) Ba điểm \(M,H,K\) thẳng hàng |
a) Xét \(\Delta OAH\)và \(\Delta OBH\)ta có:
\(OA = OB\,\,(gt)\)
OHlà cạnh chung
\(HA = HB\,\,\,(gt)\)
Vậy \(\Delta OAH = \Delta OBH\;\;\left( {c – c – c} \right)\) (đpcm)
b) Ta có: \(\Delta OAH = \Delta OBH\;\;\left( {cmt} \right) \Rightarrow \angle AOH = \angle BOH\) (hai góc tương ứng)
Xét \(\Delta AOC\)và \(\Delta BOC\)ta có:
\(\begin{array}{l}OA = OB\,\,\,(gt)\\\angle AOH = \angle BOH\;\;\left( {cmt} \right)\\OC\;\;chung\end{array}\)
Vậy \(\Delta AOC = \Delta BOC\;\;\left( {c – g – c} \right).\)
\( \Rightarrow AC = BC\) (hai cạnh tương ứng) (đpcm).
c) Xét \(\Delta OAB\) có \(OA = OB \Rightarrow \Delta OAB\) cân tại \(O.\)
Lại có \(OH\) là đường trung tuyến ứng với cạnh \(AB \Rightarrow OH\) vừa là đường cao, đường phân giác của \(\Delta OAB.\) (tính chất)
\( \Rightarrow OH \bot AB = \left\{ H \right\}\;\;hay\;\;\angle OHA = {90^0}.\)
Ta có: \(MI \bot OH\;\;\left( {gt} \right),\;\;AB \bot OH\;\;\left( {cmt} \right)\)
\( \Rightarrow MI//AB\;\;\left( {//OH} \right).\;\;\;\left( {dpcm} \right)\)
d) Xét \(\Delta MOI\) ta có: \(MI \bot OH\;\;\left( {gt} \right)\) và \(OI = IH\;\;\left( {gt} \right)\)
\( \Rightarrow MI\) vừa là đường cao, vừa là đường trung tuyến ứng với cạnh \(OH \Rightarrow \Delta OMH\) cân tại \(M.\) (tính chất)
\( \Rightarrow \angle MOI = \angle MHO\) (tính chất).
Lại có: \(\angle MOI = \angle AOH = \angle HOB\;\;\left( {cmt} \right)\)
\( \Rightarrow \angle MHI = \angle HOB\;\;\left( { = \angle MOI} \right)\)
Mà hai góc này ở vị trí so le trong \( \Rightarrow OB//MH\;\;\left( 1 \right)\)
Vì \(\Delta OAC = \Delta OBC\;\;\left( {cmt} \right) \Rightarrow \angle OAC = \angle OBC = {90^0}\) (hai góc tương ứng).
Hay \(OB \bot BC = \left\{ B \right\}.\)
Ta có: \(\left\{ \begin{array}{l}HK \bot BC\;\;\left( {gt} \right)\\OB \bot BC\;\;\left( {cmt} \right)\end{array} \right. \Rightarrow HK//OB\) (từ vuông góc đến song song) (2)
Từ (1) và (2) ta có: \(\left\{ \begin{array}{l}OB//MH\\OB//HM\end{array} \right. \Rightarrow M,\;H,\;K\) thẳng hàng (đpcm).
Bài 6: Từ \(x + y = x.y \Rightarrow x = x.y – y = y(x – 1)\)
\( \Rightarrow x:y = \dfrac{{y(x – 1)}}{y} = x – 1\) (do \(y \ne 0\)).
Theo đề bài \(x:y = x + y\), suy ra \(x – 1 = x + y \Rightarrow y = – 1\;\;\left( {tm} \right)\).
Thay \(y = – 1\) vào \(x + y = x.y\) ta được: \(x + ( – 1) = x.( – 1) \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\)
Vậy \(x = \dfrac{1}{2}\,\,;\,\,\,y = – 1\).
