Kiểm tra học kì 1 Toán lớp 7: Trong các khẳng định sau, khẳng định nào đúng?

I. PHẦN TRẮC NGHIỆM (2đ)

1. : Trong các khẳng định sau, khẳng định nào đúng?

A. \(\left| {\dfrac{{ – 1}}{5}} \right| = \dfrac{1}{5}\)

B. \(\left| {\dfrac{1}{{ – 5}}} \right| = \dfrac{1}{{ – 5}}\)

C. \(\left| {\dfrac{1}{5}} \right| = \dfrac{{ – 1}}{5}\)

D. \(\left| x \right| = x\), với mọi \(x \in \mathbb{Q}\)

2. : Cho hàm số \(y = f\left( x \right) = x – 7\). Trong các khẳng định sau, khẳng định nào đúng?

A. \(f\left( { – 2} \right) = 9\) 

B. \(f\left( { – 2} \right) =  – 5\)

C. \(f\left( { – 2} \right) =  – 9\)

D. \(f\left( { – 2} \right) = 14\)

3. : Các số x, y thỏa mãn \(\dfrac{x}{3} = \dfrac{y}{4}\)và \(x – y = 2\) là:

A. \(x = 6\,;\,y = 8\)

B. \(x =  – 6\,;\,y =  – 8\)

C. \(x = 3\,;\,y = 4\)

D. \(x =  – 3\,;\,y =  – 4\)

4. :Cho \(\Delta ABC\) có góc B= góc C = \({60^o}\), khi đó số đo góc A là:

A. \({120^o}\)             B. \({180^o}\)

C. \({90^o}\)                           D. \({60^o}\)

II. TỰ LUẬN (8đ)

1. (1,5đ):Thực hiện phép tính (bằng cách hợp lý nếu có thể)

a) \(\dfrac{1}{2}.\dfrac{8}{3} – \dfrac{{ – 1}}{9}\)

b) \(\dfrac{7}{{13}} – 1\dfrac{2}{{29}} – \dfrac{7}{{13}} + 1,25 + \dfrac{2}{{29}}\)

c) \(\dfrac{{ – 13}}{8}.\dfrac{7}{{19}} + \dfrac{5}{8}.\dfrac{7}{{19}}\)

d)\( – {2^2}.\sqrt {{{\left( { – 3} \right)}^2} + {4^2}}  – 1\dfrac{1}{3}:2\dfrac{2}{3}\)

2. (1,5đ):Tìm x:

a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)

b) \(\dfrac{1}{6}x – 3 = \dfrac{{ – 2}}{3}\)

c) \({\left( {\dfrac{1}{5} – x} \right)^2} = \dfrac{{16}}{9}\)

d) \(\dfrac{{x – 1}}{6} = \dfrac{{x + 3}}{5}\)

3. (1,5đ): Cho biết để hoàn thành công việc trong 10 giờ thì cần 48 người làm. Hỏi nếu chỉ có 40 người làm thì mất bao nhiêu thời gian để hoàn thành công việc đó? (Năng suất làm việc của mỗi công nhân là như nhau).

4. (3đ):Cho góc nhọn mOn, Ot là tia phân giác của góc mOn. Trên tia Om và On lần lượt lấy hai điểm C và D sao cho OC = OD. Đoạn thẳng CD cắt Ot tại P.

a) Chứng minh \(\Delta OCP = \Delta ODP\).

b) Chứng minh \(CP = DP\)và \(OP \bot CD\).

c) Trên tia Ot lấy điểm Q sao cho P là trung điểm của OQ. Chứng minh CQ // OD.

5. (0,5đ): Cho năm số tự nhiên a, b, c, d, e thỏa mãn \({a^b} = {b^c} = {c^d} = {d^e} = {e^a}\). Chứng minh rằng năm số a, b, c, d, e bằng nhau.

I. TRẮC NGHIỆM

II. TỰ LUẬN

1. Thực hiện phép tính (bằng cách hợp lý nếu có thể)

a) \(\dfrac{1}{2}.\dfrac{8}{3} – \dfrac{{ – 1}}{9} \)

\(= \dfrac{4}{3} + \dfrac{1}{9} = \dfrac{{4.3 + 1}}{9} = \dfrac{{13}}{9}\)

b) \(\dfrac{7}{{13}} – 1\dfrac{2}{{29}} – \dfrac{7}{{13}} + 1,25 + \dfrac{2}{{29}} \)

\(= \left( {\dfrac{7}{{13}} – \dfrac{7}{{13}}} \right) + \left( { – \dfrac{{31}}{{29}} + \dfrac{2}{{29}}} \right) + \dfrac{{125}}{{100}} \)

\(=  – 1 + \dfrac{5}{4} = \dfrac{1}{4}\)

c) \(\dfrac{{ – 13}}{8}.\dfrac{7}{{19}} + \dfrac{5}{8}.\dfrac{7}{{19}}\)

\(= \dfrac{7}{{19}}.\left( {\dfrac{{ – 13}}{8} + \dfrac{5}{8}} \right) \)

\(= \dfrac{7}{{19}}.\left( { – 1} \right) = \dfrac{{ – 7}}{{19}}\)

d) \( – {2^2}.\sqrt {{{\left( { – 3} \right)}^2} + {4^2}}  – 1\dfrac{1}{3}:2\dfrac{2}{3}\)

\(=  – 4.\sqrt {9 + 16}  – \dfrac{4}{3}.\dfrac{3}{8} \)

\(=  – 4.5 – \dfrac{1}{2} =  – 20 – \dfrac{1}{2} = \dfrac{{ – 41}}{2}\)

2. Tìm x:

a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)

\(\Leftrightarrow x = \dfrac{3}{{10}} – \dfrac{2}{5} = \dfrac{{3 – 2.2}}{{10}} = \dfrac{{ – 1}}{{10}}\)

b) \(\dfrac{1}{6}x – 3 = \dfrac{{ – 2}}{3}\)

\(\Leftrightarrow \dfrac{1}{6}x = \dfrac{{ – 2}}{3} + 3 = \dfrac{7}{3}\)

\(\Leftrightarrow x = \dfrac{7}{3}.6 = 14\)

c) \({\left( {\dfrac{1}{5} – x} \right)^2} = \dfrac{{16}}{9} \)

\(\Leftrightarrow \left| {\dfrac{1}{5} – x} \right| = \dfrac{4}{3}\)

\( \Leftrightarrow \left[ \begin{array}{l}\dfrac{1}{5} – x = \dfrac{4}{3}\\\dfrac{1}{5} – x =  – \dfrac{4}{3}\end{array} \right.\)

\(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{5} – \dfrac{4}{3}\\x = \dfrac{1}{5} + \dfrac{4}{3}\end{array} \right. \)

\(\Leftrightarrow \left[ \begin{array}{l}x =  – \dfrac{{17}}{{15}}\\x = \dfrac{{23}}{{15}}\end{array} \right..\)

\(\begin{array}{l}d)\;\;\dfrac{{x – 1}}{6} = \dfrac{{x + 3}}{5}\\ \Leftrightarrow 5.\left( {x – 1} \right) = 6.\left( {x + 3} \right)\\ \Leftrightarrow 5x – 5 = 6x + 18\\ \Leftrightarrow 6x – 5x =  – 5 – 18\\ \Leftrightarrow x =  – 23\end{array}\)

3. Gọi thời gian để hoàn thành công việc đó nếu chỉ có 40 người làm là x(giờ) (\(x > 10\))

Vì số người làm và thời gian để hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên:

\(10.48 = x.40 \Leftrightarrow x = \dfrac{{480}}{{40}} = 12\)(giờ)

Vậy nếu chỉ có 40 người làm thì mất 12 giờ để hoàn thành công việc đó.

4.

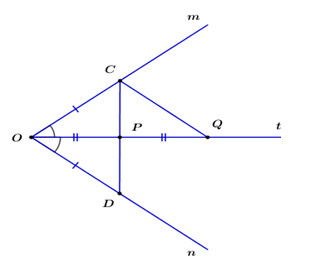
Cho góc nhọn mOn, Ot là tia phân giác của góc mOn. Trên tia Om và On lần lượt lấy hai điểm C và D sao cho OC = OD. Đoạn thẳng CD cắt Ot tại P.

a) Chứng minh \(\Delta OCP = \Delta ODP\).

Xét \(\Delta OCP\)và \(\Delta ODP\) có:

OP chung

\(\angle COP = \angle DOP\) (Ot là tia phân giác của góc mOn)

OC = OD (gt)

\( \Rightarrow \Delta OCP = \Delta ODP\)  (c.g.c)

b) Chứng minh \(CP = DP\) và \(OP \bot CD\)

Xét \(\Delta ODC\) có OC = OD (gt) \( \Rightarrow \Delta OCD\) cân tại O (đn)

\( \Rightarrow \)OP vừa là phân giác góc O vừa là đường cao và trung tuyến trong \(\Delta ODP\)

\( \Rightarrow \)\(CP = DP\) và \(OP \bot CD\) (đpcm).

c) Trên tia Ot lấy điểm Q sao cho P là trung điểm của OQ. Chứng minh CQ // OD.

Xét \(\Delta ODP\) và \(\Delta QCP\) có:

\(CP = DP\) (cmt)

\(\angle OPD = \angle QPC\) (đối đỉnh)

PO = PQ (P là trung điểm của OQ)

\( \Rightarrow \Delta ODP = \Delta QCP\)  (c.g.c)\( \Rightarrow \angle ODP = \angle QCP\) (góc tương ứng)

Mà hai góc này ở vị trí so le trong\( \Rightarrow CQ//OD\)(đpcm)

5. Giả sử hai trong số 5 số tự nhiên đã cho không bằng nhau: \(a < b\) (1)

Trong hai lũy thừa bằng nhau thì lũy thừa có cơ số nhỏ hơn sẽ có số mũ lớn hơn và ngược lại.

Có \({a^b} = {b^c}\) mà \(a < b \Rightarrow b > c\)

Có\({b^c} = {c^d}\) mà \(b > c \Rightarrow c < d\)

Có \({c^d} = {d^e}\) mà \(c < d \Rightarrow d > e\)

Có \({d^e} = {e^a}\)mà \(d > e \Rightarrow e < a\)

Có \({e^a} = {a^b}\) mà \(e < a \Rightarrow a > b\)(2)

Từ (1) và (2) \( \Rightarrow \) giả thiết sai

Vậy \(a = b = c = d = e\) (đpcm)