Đề kiểm tra học kì 1 môn Toán lớp 7: Từ C vẽ đường vuông góc với BC cắt AB tại E. Chứng minh EC // AKvà tính số đo góc AEC?

Bài 1 : (2,0đ) Tính giá trị của biểu thức bằng cách hợp lý (nếu có thể):

\(a)\;\left| { – 3} \right| + \left| { – 2,65} \right| – \left| 0 \right|\)

\(b)\;{\left( { – 3} \right)^3}.\dfrac{{11}}{{45}} + {\left( { – 3} \right)^3}.\dfrac{4}{{45}}\)

\(c)\;\sqrt {25} .\dfrac{1}{{10}} + {\left( {\dfrac{{ – 1}}{2}} \right)^2}\)

\(d)\; – \left( {23,5.5 + 19,6} \right) + 5.23,5 – \left( {6 – 19,6} \right)\)

Bài 2 : (2,0đ) Tìm x biết:

\(a)\;x + \dfrac{1}{4} =  – \dfrac{3}{5}\)

\(b)\;\left| {x – 3} \right| – 2 = 0\)

\(c)\;{\left( {3{\rm{x}} – 2} \right)^5} =  – 243\)

\(d)\;\left| {x + 5} \right| + 6 = 9\)

Bài 3 : (2,0đ) Ba lớp 7A, 7B, 7C có số học sinh giỏi tỉ lệ với 2; 4; 6. Tính số học sinh giỏi của mỗi lớp, biết rằng số học sinh giỏi lớp 7C nhiều hơn số học sinh giỏi lớp 7B là 6 em.

Bài 4(3,0đ)

Cho \(\Delta ABC\) vuông tại A có AB = AC. Gọi K là trung điểm của BC.

a) Chứng minh rằng\(\Delta AKB = \Delta AKC\).

b) Chứng minh\(AK \bot BC\).

c) Từ C vẽ đường vuông góc với BC cắt AB tại E. Chứng minh EC // AKvà tính số đo góc AEC?

Bài 5 : (1,0đ) Cho \(\dfrac{{2{\rm{x}} – 4y}}{3} = \dfrac{{4{\rm{z}} – 3{\rm{x}}}}{2} = \dfrac{{3y – 2{\rm{z}}}}{4}\). Tìm x, y, z biết \(2{\rm{x}} – y + z = 27\).

Bài 1: \(\begin{array}{l}a)\;\left| { – 3} \right| + \left| { – 2,65} \right| – \left| 0 \right| \\= 3 + 2,65 + 0 = 5,65\\b)\;{\left( { – 3} \right)^3}.\dfrac{{11}}{{45}} + {\left( { – 3} \right)^3}.\dfrac{4}{{45}}\\ = {( – 3)^3}.\left( {\dfrac{{11}}{{45}} + \dfrac{4}{{45}}} \right) \\= ( – 27).\dfrac{{15}}{{45}} = ( – 27).\dfrac{1}{3} =  – 9\\c)\;\sqrt {25} .\dfrac{1}{{10}} + {\left( {\dfrac{{ – 1}}{2}} \right)^2} \\= \sqrt {{5^2}} .\dfrac{1}{{10}} + \dfrac{1}{4} \\= 5.\dfrac{1}{{10}} + \dfrac{1}{4} = \dfrac{1}{2} + \dfrac{1}{4}\\ = \dfrac{{1.2}}{{2.2}} + \dfrac{1}{4} = \dfrac{{2 + 1}}{4} = \dfrac{3}{4}\\d)\; – \left( {23,5.5 + 19,6} \right) + 5.23,5 – \left( {6 – 19,6} \right)\\ =  – 23,5.5 – 19,6 + 23,5.5 – 6 + 19,6 =  – 6\end{array}\)

Bài 2: \(a)\;x + \dfrac{1}{4} =  – \dfrac{3}{5}\\ \Leftrightarrow x =  – \dfrac{3}{5} – \dfrac{1}{4}\\ \Leftrightarrow x = \dfrac{{ – 3.4}}{{5.4}} – \dfrac{{1.5}}{{4.5}} = \dfrac{{ – 12 – 5}}{{20}} = \dfrac{{ – 17}}{{20}}\)

Vậy \(x = \dfrac{{ – 17}}{{20}}\).

\(b)\;\left| {x – 3} \right| – 2 = 0\)

Cách 1:

– Nếu \(x – 3 \ge 0\) tức \(x \ge 3\) thì \(\left| {x – 3} \right| = x – 3\). Ta có:

\(x – 3 – 2 = 0 \Leftrightarrow x – 5 = 0 \Leftrightarrow x = 5\) (Thỏa mãn điều kiện\(x \ge 3\))

– Nếu\(x – 3 < 0 \Leftrightarrow x < 3\) thì \(\left| {x – 3} \right| = 3 – x.\)Ta có:

\(3 – x – 2 = 0 \Leftrightarrow 1 – x = 0 \Leftrightarrow x = 1\)(Thỏa mãn điều kiện \(x < 3\))

Vậy x = 5 hoặc x = 1.

Cách 2:

\(\left| {x – 3} \right| – 2 = 0\\ \Leftrightarrow \left| {x – 3} \right| = 2 \\\Leftrightarrow \left[ \begin{array}{l}x – 3 = 2\\x – 3 =  – 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2 + 3\\x =  – 2 + 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 1\end{array} \right..\)

Vậy x = 5 hoặc x = 1.

\(\begin{array}{l}c)\;{\left( {3{\rm{x}} – 2} \right)^5} =  – 243\\ \Leftrightarrow {\left( {3{\rm{x}} – 2} \right)^5} = {\left( { – 3} \right)^5} \\\Leftrightarrow 3{\rm{x}} – 2 =  – 3\\ \Rightarrow 3{\rm{x}} =  – 3 + 2 =  – 1 \\\Leftrightarrow x = \dfrac{{ – 1}}{3}\end{array}\)

Vậy \(x =  – \dfrac{1}{3}.\)

\(\begin{array}{l}d)\;\left| {x + 5} \right| + 6 = 9\\ \Leftrightarrow \left| {x + 5} \right| = 3\\ \Leftrightarrow \left[ \begin{array}{l}x + 5 = 3\\x + 5 =  – 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  – 2\\x =  – 8\end{array} \right..\end{array}\)

Vậy \(x =  – 2\) hoặc \(x =  – 8.\)

Bài 3: Gọi số học sinh giỏi của 3 lớp 7A, 7B, 7C lần lượt là \(x,\;y,\;z\;\;\left( {x,\;y,\;z \in {N^*},\;y < z,\;z > 6} \right).\)

Học sinh giỏi ở 3 lớp tỉ lệ với 2; 4; 6. Từ đây ta có:\(\)\(\dfrac{x}{2} = \dfrac{y}{4} = \dfrac{z}{6}\)

Biết rằng số học sinh giỏi lớp 7C nhiều hơn số học sinh giỏi lớp 7B là 6 em nên \(z – y = 6.\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\dfrac{x}{2} = \dfrac{y}{4} = \dfrac{z}{6} = \dfrac{{z – y}}{{6 – 4}} = \dfrac{6}{2} = 3\\ \Rightarrow \left\{ \begin{array}{l}x = 2.3 = 6\\y = 3.4 = 12\\z = 3.6 = 18\end{array} \right..\end{array}\)

Vậy số học sinh giỏi của 3 lớp 7A, 7B, 7C lần lượt là 6 học sinh, 12 học sinh, 18 học sinh.

Bài 4:

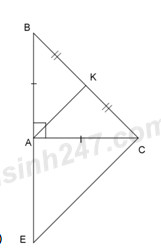
a) Theo đề bài ta có: \(\Delta ABC\) vuông tại A và AB = AC.

\( \Rightarrow \Delta ABC\) vuông cân tại A.

\( \Rightarrow \angle ABK = \angle ACK = {45^0}\)(2 góc đáy bằng nhau)

Xét \(\Delta AKB\) và \(\Delta AKC\) ta có:

BK = KC (K là trung điểm của BC)

AB = AC (gt)

\(\angle ABK = \angle ACK\) (cmt)

\( \Rightarrow \Delta AKB = \Delta AKC\;(c – g – c)\) (đpcm)

b) Ta có \(\Delta AKB = \Delta AKC\;(c – g – c)\)

\( \Rightarrow \angle AKB = \angle AKC\) (2 góc tương ứng)

Mà \(\angle BKC = \angle BK{\rm{A}} + \angle AKC = {180^0}\) (góc bẹt)

\( \Rightarrow \angle BK{\rm{A}} = \angle AKB = \angle AKC = \dfrac{1}{2}\angle BKC = \dfrac{{{{180}^0}}}{2} = {90^0}\)

\( \Rightarrow AK \bot BC\) (đpcm)

c) Theo bài ta có: \(EC \bot BC\)

Lại có: \(AK \bot BC\) (chứng minh trên)

\( \Rightarrow EC//\;AK\) (từ vuông góc đến song song) (đpcm)\(\)

Vì \(EC//AK\)  nên \(\angle BAK = \angle A{\rm{EC}}\)  (cặp góc đồng vị bằng nhau) (1)

Xét \(\Delta AKB\) có:

\(\angle ABK + \angle BK{\rm{A}} + \angle K{\rm{A}}B = {180^0}\)(Tổng 3 góc trong một tam giác bằng 180⁰)

\(\begin{array}{l} \Leftrightarrow {45^0} + {90^0} + \angle K{\rm{A}}B = {180^0}\\ \Leftrightarrow \angle K{\rm{A}}B = {45^0}\\ \Rightarrow \angle BAK = \angle K{\rm{A}}B = {45^0}\;\;\;\;\;\left( 2 \right)\end{array}\)

Từ (1) và (2) ta có: \(\angle AEC = {45^0}\).\(\angle MFP = {45^0}\)

Bài 5: Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\;\;\;\;\;\dfrac{{2{\rm{x}} – 4y}}{3} = \dfrac{{4{\rm{z}} – 3{\rm{x}}}}{2} = \dfrac{{3y – 2{\rm{z}}}}{4}\\ \Leftrightarrow \dfrac{{(2{\rm{x}} – 4y).3}}{{3.3}} = \dfrac{{(4{\rm{z}} – 3{\rm{x}}).2}}{{2.2}} = \dfrac{{(3y – 2{\rm{z)}}{\rm{.4}}}}{{4.4}}\\ \Leftrightarrow \dfrac{{6{\rm{x}} – 12y}}{9} = \dfrac{{8{\rm{z}} – 6{\rm{x}}}}{4} = \dfrac{{12y – 8{\rm{z}}}}{{16}} = \dfrac{{6{\rm{x}} – 12y + 8{\rm{z}} – 6{\rm{x}} + 12y – 8{\rm{z}}}}{{9 + 4 + 16}} = \dfrac{0}{{29}}\\ \Rightarrow \left\{ \begin{array}{l}6{\rm{x}} – 12y = 0\\8{\rm{z}} – 6{\rm{x}} = 0\\12y – 8z = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2{\rm{x}} = 4y\\4{\rm{z}} = 3{\rm{x}}\\{\rm{3y}}\;{\rm{ = }}\;{\rm{2z}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{x}{4} = \dfrac{y}{2}\\\dfrac{z}{3} = \dfrac{x}{4}\end{array} \right.\\ \Rightarrow \dfrac{x}{4} = \dfrac{y}{2} = \dfrac{z}{3}\end{array}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\;\;\;\;\dfrac{x}{4} = \dfrac{y}{2} = \dfrac{z}{3}\\ \Leftrightarrow \dfrac{{2x}}{8} = \dfrac{{ – y}}{{ – 2}} = \dfrac{z}{3} = \dfrac{{2{\rm{x}} – y + z}}{{8 – 2 + 3}} = \dfrac{{27}}{9} = 3\\ \Rightarrow \left\{ \begin{array}{l}x = 3.4 = 12\\y = 2.3 = 6\\z = 3.3 = 9\end{array} \right..\end{array}\)

Vậy \(x = 12;\;y = 6;\;z = 9.\)