Đề kiểm tra học kì 1 môn Toán lớp 7: Gọi A là trung điểm của DF, vẽ điểm B sao cho A là trung điểm của EB. Chứng minh F là trung điểm của CB.

1. (1đ): a) Cho y tỉ lệ thuận với x, biết \(x =  – 8\)thì \(y = \dfrac{2}{3}\). Tính hệ số tỉ lệ k.

b) Cho y tỉ lệ nghịch với x, biết \(x = \dfrac{{ – 4}}{3}\)thì \(y =  – 12\). Tính hệ số tỉ lệ a.

2. (1,5đ):Tính hợp lý (nếu có thể)

a) \(\dfrac{{ – 2}}{3} + 75\%  – 5\dfrac{1}{4} + {\left( {2006} \right)^0}\)

b) \(3\dfrac{2}{5} – 2\dfrac{2}{5} – {\left( {\dfrac{{ – 1}}{2}} \right)^3} + 2\dfrac{1}{2}:\sqrt {\dfrac{{25}}{9}} \)

3. (2đ):Tìm x biết

a) \(2x – \dfrac{1}{3} =  – \dfrac{2}{5}\)

b) \(1\dfrac{4}{5} – \left| {x + \dfrac{3}{2}} \right| = 0,25\)

c) \(\dfrac{{2x – 1}}{{ – 3}} = \dfrac{{3x + 2}}{5}\)

4. (2đ): Hưởng ứng phong trào: “Phát triển văn hóa đọc trong kỷ nguyên số”, ba lớp 7A, 7B, 7C đóng góp cho thư viện nhà trường được 300 quyển sách. Biết rằng số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C tỉ lệ với 5; 3; 7. Tính số sách đóng góp cho thư viện của mỗi lớp.

5. (3,5đ):  Cho tam giác DEF, lấy I là trung điểm cạnh EF. Trên tia đối của tia ID, lấy điểm C sao cho IC = ID. Chứng minh rằng:

a) \(\Delta DIE = \Delta CIF\).

b) DE // CF

c) Kẻ \(DH \bot EF,\,\,CK \bot EF\) ( H, K thuộc EF). Chứng minh \(EK = HF\).

d) Gọi A là trung điểm của DF, vẽ điểm B sao cho A là trung điểm của EB. Chứng minh F là trung điểm của CB.

6. (0,5đ): Cho các số a, b, c thỏa mãn: \(3\left( {a + b} \right) = 2\left( {b + c} \right) = 7\left( {c + a} \right)\)

Chứng minh rằng: \(\dfrac{{c – a}}{7} = \dfrac{{b – c}}{8}.\)

1. a) Cho y tỉ lệ thuận với x, biết \(x =  – 8\) thì \(y = \dfrac{2}{3}\). Tính hệ số tỉ lệ k.

Vì y tỉ lệ thuận với\(x \Rightarrow k = \dfrac{y}{x} = \dfrac{2}{{3.\left( { – 8} \right)}} =  – \dfrac{1}{{12}}\)

b) Cho y tỉ lệ nghịch với x, biết \(x = \dfrac{{ – 4}}{3}\) thì \(y =  – 12\). Tính hệ số tỉ lệ a.

Vì y tỉ lệ nghịch với \(x \Rightarrow a = x.y = \dfrac{{ – 4}}{3}.\left( { – 12} \right) = 16\)

2. Tính hợp lý (nếu có thể)

a) \(\dfrac{{ – 2}}{3} + 75{\raise0.5ex\hbox{$\scriptstyle o$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle o$}} – 5\dfrac{1}{4} + {\left( {2016} \right)^0}\)

\(= \dfrac{{ – 2}}{3} + \dfrac{3}{4} – \dfrac{{21}}{4} + 1 \)

\(= \dfrac{{ – 2}}{3} – \dfrac{9}{2} + 1 \)

\(= \dfrac{{ – 2.2 – 9.3 + 1.6}}{6} = \dfrac{{ – 25}}{6}\)

b) \(3\dfrac{2}{5} – 2\dfrac{2}{5} – {\left( {\dfrac{{ – 1}}{2}} \right)^3} + 2\dfrac{1}{2}:\sqrt {\dfrac{{25}}{9}}  \)

\(= 3 + \dfrac{2}{5} – 2 – \dfrac{2}{5} + \dfrac{1}{8} + \dfrac{5}{2}:\dfrac{5}{3} \)

\(= 1 + \dfrac{1}{8} + \dfrac{3}{2} = \dfrac{{1.8 + 1 + 3.4}}{8} = \dfrac{{21}}{8}\)

3. Tìm x biết

\(a)\;\;2x – \dfrac{1}{3} =  – \dfrac{2}{5}\\ \Leftrightarrow 2x =  – \dfrac{2}{5} + \dfrac{1}{3} = \dfrac{{ – 2.3 + 1.5}}{{15}} = \dfrac{{ – 1}}{{15}}\\ \Leftrightarrow x = \dfrac{{ – 1}}{{15}}:2 = \dfrac{{ – 1}}{{30}}\)

\(b)\;1\dfrac{4}{5} – \left| {x + \dfrac{3}{2}} \right| = 0,25 \\\Leftrightarrow \left| {x + \dfrac{3}{2}} \right| = \dfrac{9}{5} – \dfrac{1}{4} = \dfrac{{9.4 – 1.5}}{{20}} = \dfrac{{31}}{{20}}\)

TH1: \(x + \dfrac{3}{2} = \dfrac{{31}}{{20}}\\ \Leftrightarrow x = \dfrac{{31}}{{20}} – \dfrac{3}{2} = \dfrac{{31 – 3.10}}{{20}} = \dfrac{1}{{20}}\)

TH2: \(x + \dfrac{3}{2} =  – \dfrac{{31}}{{20}}\\ \Leftrightarrow x =  – \dfrac{{31}}{{20}} – \dfrac{3}{2} = \dfrac{{ – 31 – 3.10}}{{20}} = \dfrac{{ – 61}}{{20}}\)

\(\begin{array}{l}c)\;\;\dfrac{{2x – 1}}{{ – 3}} = \dfrac{{3x + 2}}{5}\\ \Leftrightarrow 5.\left( {2x – 1} \right) =  – 3.\left( {3x + 2} \right)\\ \Leftrightarrow 10x – 5 =  – 9x – 6 \\\Leftrightarrow 19x =  – 1 \Leftrightarrow x = \dfrac{{ – 1}}{{19}}\end{array}\)

4. Hưởng ứng phong trào: “Phát triển văn hóa đọc trong kỷ nguyên số”, ba lớp 7A, 7B, 7C đóng góp cho thư viện nhà trường được 300 quyển sách. Biết rằng số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C tỉ lệ với 5; 3; 7. Tính số sách đóng góp cho thư viện của mỗi lớp.

Gọi số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C lần lượt là a, b, c (a, b, c\( \in {\mathbb{N}^*}\); a , b, c< 300)

Ba lớp 7A, 7B, 7C đóng góp cho thư viện nhà trường được 300 quyển sách nên: \(a + b + c = 300\)  (1)

Số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C tỉ lệ với 5; 3; 7 nên:

\(a:b:c = 5:3:7 \Rightarrow \dfrac{a}{5} = \dfrac{b}{3} = \dfrac{c}{7}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\dfrac{a}{5} = \dfrac{b}{3} = \dfrac{c}{7} = \dfrac{{a + b + c}}{{5 + 3 + 7}} = \dfrac{{300}}{{15}} = 20\\ \Rightarrow \left\{ \begin{array}{l}a = 20.5 = 100\;\;\;\left( {tm} \right)\\b = 20.3 = 60\;\;\;\;\;\left( {tm} \right)\\c = 20.7 = 140\;\;\;\;\left( {tm} \right)\end{array} \right..\end{array}\)

Vậy ba lớp 7A, 7B, 7C đóng góp cho thư viện lần lượt 100, 60, 140 quyển sách.

5.

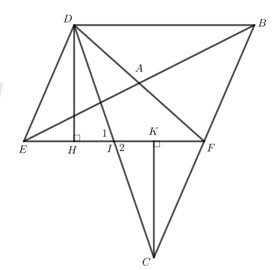
Cho tam giác DEF, lấy I là trung điểm cạnh EF. Trên tia đối của tia ID, lấy điểm C sao cho IC = ID. Chứng minh rằng:

a) \(\Delta DIE = \Delta CIF\).

Xét \(\Delta DIE\) và \(\Delta CIF\)có:

\(ID = IC\) (gt);

\(\angle {I_1} = \angle {I_2}\)(đối đỉnh);

\(IE = IF\) (I là trung điểm cạnh EF)

\( \Rightarrow \Delta DIE = \Delta CIF\) (c.g.c) (đpcm)

b) DE // CF

Có \(\Delta DIE = \Delta CIF\)(cmt) \( \Rightarrow \angle EDI = \angle FCI\) (2 góc tương ứng)

Mà 2 góc này ở vị trí so le trong

\( \Rightarrow \)DE // CF

c) Kẻ \(DH \bot EF,\,\,CK \bot EF\) ( H, K thuộc EF). Chứng minh \(EK = HF\).

Xét \(\Delta DHI\) và \(\Delta CKI\) có:

\(ID = IC\) (gt);

\(\angle {I_1} = \angle {I_2}\) (đối đỉnh);

\(\angle DHI = \angle CKI\,\,( = {90^o})\)

\( \Rightarrow \Delta DHI = \Delta CKI\)(ch.gn)\( \Rightarrow HI = KI\) (2 cạnh tương ứng)

Mặt khác \(IF = IE\) (I là trung điểm cạnh EF)

\( \Rightarrow HI + IF = KI + IE\) hay  \(HF = EK\) (đpcm)

d) Gọi A là trung điểm của DF, vẽ điểm B sao cho A là trung điểm của EB. Chứng minh F là trung điểm của CB.

Xét \(\Delta DAE\) và \(\Delta FAB\) có:

\(AD = AF\) (A là trung điểm của DF);

\(AE = AB\) (A là trung điểm của EB);

\(\angle DAE = \angle FAB\,\,\)(đối đỉnh)

\( \Rightarrow \Delta DAE = \Delta FAB\)(c.g.c)

\( \Rightarrow \angle EDA = \angle BFA\) (2 góc tương ứng)

Mà hai góc này ở vị trí so le trong

\( \Rightarrow \)DE // BF mặt khác DE // CF (cmt)

\( \Rightarrow \)C, B, F thẳng hàng (tiên đề Ơclit)

Lại có \(DE = BF\) (DEFB là hình bình hành); \(DE = CF\) (\(\Delta DIE = \Delta CIF\))

\( \Rightarrow BF = CF\,\,\,( = DE)\)

\( \Rightarrow \)F là trung điểm của CB.

6. Cho các số a, b, c thỏa mãn: \(3\left( {a + b} \right) = 2\left( {b + c} \right) = 7\left( {c + a} \right)\)

Chứng minh rằng: \(\dfrac{{c – a}}{7} = \dfrac{{b – c}}{8}.\)

Ta có:

\(3\left( {a + b} \right) = 2\left( {b + c} \right)\)

\(\Leftrightarrow 3a + 3b = 2b + 2c\)

\(\Leftrightarrow 3a + b = 2c \)

\(\Leftrightarrow 12a + 4b = 8c\) (1)

\(3\left( {a + b} \right) = 7\left( {c + a} \right)\)

\(\Leftrightarrow 3a + 3b = 7c + 7a \)

\(\Leftrightarrow  – 4a + 3b = 7c\) (2)

Cộng lần lượt hai vế của (1) và (2) với nhau ta được:

\(8a + 7b = 15c\)

\(\Leftrightarrow 8a + 7b = 8c + 7c\)

\(\Leftrightarrow 8c – 8a = 7b – 7c\)

\( \Leftrightarrow 8\left( {c – a} \right) = 7\left( {b – c} \right)\)

\(\Leftrightarrow \dfrac{{c – a}}{7} = \dfrac{{b – c}}{8}\)(đpcm)