Trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh(c.g.c): bài 24, 25, 26 trang 118; 27 trang 119; Bài 28,29, 30,31,32 trang 120 SGK Toán 7 – Hình học chương 2.
24. Vẽ ΔABC biết ∠A = 900; AB = AC = 3cm. Sau đó đo các ∠B và ∠C.
Cách vẽ: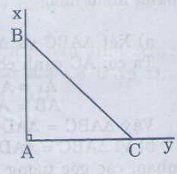
– Vẽ ∠xAy = 900
– Trên tia Ax vẽ đoạn thẳng AB = 3cm,
– Trên tia Ay vẽ đoạn thẳng AC = 3cm,
– Vẽ đoạn BC.
Ta vẽ được đoạn thẳng BC.
Ta đo các ∠B và ∠C ta được ∠B = ∠C = 450
25. Trên mỗi hình 82,83,84 sau có các tam giác nào bằng nhau? Vì sao?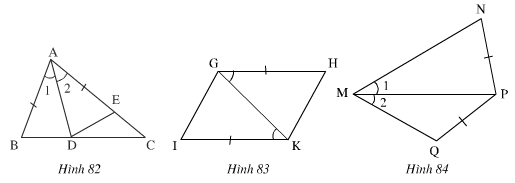
Hình 82: ∆ADB và ∆ADE có: AB = AE (gt)
∠A1b= ∠A2 , AD chung.
Nên ∆ADB = ∆ADE(c.g.c)
Hình 83: ∆HGK và ∆IKG có:
HG = IK (gt)
∠G = ∠K (gt)
GK là cạnh chung (gt)
nên ∆HGK = ∆IKG( c.g.c)
Hình 84: ∆PMQ và ∆PMN có: MP cạnh chung
∠M1 = ∠M2
Nhưng MN không bằng MQ. Nên PMQ không bằng PMN.
26. Xét bài toán: Cho ΔABC, M là trung điểm của BC, Trên tia đối của MA lấy điểm E sao cho ME=MA. Chứng minh rẳng AB//CE”.
Dưới đây là hình vẽ và giả thiết, kết luận của bài toán(h.85)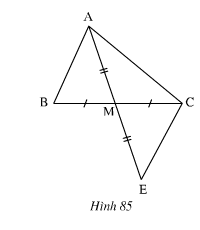
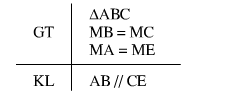
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên:
1) MB = MC(gt)
∠AMB = ∠EMC (Hai góc đối đỉnh)
MA = ME(Giả thiết)
2) Do đó ∆AMB=∆EMC(c.g.c)
3) ∠MAB = ∠MEC
⇒ AB//CE (hai ∠ bằng nhau ở vị trí sole trong)
Advertisements (Quảng cáo)
4) ∆AMB= ∆EMC⇒ ∠MAB = ∠MEC (Hai ∠ tương ứng)
5) ∆AMB và ∆EMC có:
HD: Thứ tự sắp xếp hợp lý nhất là: 5,1,2,4,3.
Luyện tập 1: Bài 27, 28, 29 trang 119, 120 (Toán 7 tập 1)
27.Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai Δ bằng nhau theo trường hợp cạnh-góc- cạnh.
a) ∆ABC= ∆ADC (h.86);
b) ∆AMB= ∆EMC (h.87)
c) ∆CAB= ∆DBA.(h.88)
a) Bổ sung thêm ∠BAC = ∠DAC để ∆ABC = ∆ADC
Vì ta có AB = AD (gt) ; và AC cạnh chung.
b) Bổ sung thêm MA = ME để ∆AMB= ∆EMC
Vì ta có ∠AMB = ∠EMC (gt); MN = MC (gt)
c) Bổ sung thêm AC = BD để ∆CAB= ∆DBA
Vì ta có 2 ΔCAB và ΔDBA là 2 Δvuông, Cạnh AB chung.
Bài 28. Trên hình 89 có bao nhiêu tam giác bằng nhau.
ΔDKE có: ∠D + ∠K + ∠E = 1800 (tổng ba ∠ trong của Δ).
hay ∠D + +800 +400 = 1800
Advertisements (Quảng cáo)
⇒∠D = 1800 -1200 = 600
Xét ∆ ABC và ∆KDE có:
AB = KD(gt)
∠B = ∠D ( cùng = 600 )
và BE = ED (gt)
Do đó ∆ABC= ∆KDE (c.g.c)
ΔMNP không có góc xem giữa hai cạnh ΔKDE ha ABC nên không bằng hai Δ còn lại .
Bài 29 trang 120. Cho ∠xAy. Lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh rằng ∆ABC = ∆ADE.
AB = AD ( gt)
BE = DC (gt)
=> AB + BE = AD + DC
Hay AE = AC
Xét ΔABC và ΔADE, ta có :
AB = AD ( gt)
∠A chung.
AC = AE (cmt).
⇒ ∆ABC = ∆ADE (c.g.c)
Luyện tập 2: Bài 30,31,32 sách trang 120
Bài 30.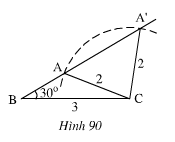
Trên hình 90, các ΔABC và ΔA’B’C’ có cạnh chung là BC=3cm. CA= CA’= 2cm, ∠ABC = ∠A’BC nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không thế áp dùng trường hợp c.g.c để kết luận hai tam giác bằng nhau.
HD. ∠ABC không phải là ∠xen giữa BC và CA,
∠A’BC không phải là ∠xen giữa hai cạnh BC và CA’.
Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A’B’C’ được.
Bài 31. Cho độ dài đoạn thẳng AB, điểm nằm trên đường trung trực của AB, so sánh độ dài các đoạn MA,MB.
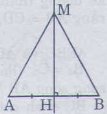Goi H là trung giao điểm của đường trung trực với đoạn AB.
Ta có
AH = BH(gt)
∠AHM = ∠BHM
MH cạnh chung
∆AHM=∆BHM(c .g.c )
Vậy MA= MB (hai cạnh tương ứng).
Bài 32. Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó.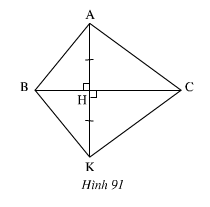
∆AHB và ∆KBH có
AH = KH(gt)
∠AHB = ∠KHB
BH cạnh chung.
nên ∆AHB=∆KBH(c.g.c)
suy ra: ∠ABH = ∠KBH
Vậy BH là tia phân giác của ∠B.
Tương tự :
∆AHC và ∆KHC
AH = HK (gt)
∠AHC = ∠KHC
HC cạnh chung
nên ∆AHC = ∆KHC(c.g.c)
Suy ra: ∠ACH = ∠KCH
Vậy CH là tia phân giác của ∠C
![[Phòng GD Phú Giáo] thi cuối học kì 2 môn Văn lớp 7: Qua nội dung đoạn văn, em học tập được điều gì từ đức tính của Bác?](https://dethikiemtra.com/wp-content/uploads/2020/06/văn-7-100x75.jpg)
