Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh(c.c.c) (Chương 2 hình học 7).
Dethikiemtra hướng dẫn làm và giải bài 15,16,17, 18, 19 trang 114; bài 20,21,22 trang 115; Bài 23 trang 116 trong sách giáo khoa.
15. ΔMNP, biết MN=2,5 cm, NP=3cm, PM= 5cm,
Các bước lần lượt như sau:
– Dùng thước vẽ đoạn MN = 2,5cm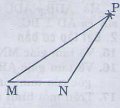
– Trên cùng một nửa mặt phẳng bở MN, dùng Compa vẽ cung tròn tâm M bán kính 5cm và cung tròn tâm N bán kinh 3cm.
– Hai cung tròn cắt nhau tại P. Vẽ các đoạn MN, NP, ta được ΔMNP (hình vẽ).
16.Vẽ tam giác biết độ dài mỗi cạnh là 3 cm. Sau đó đo góc của mỗi tam giác.
Cách vẽ ΔABC tương tự như cách vẽ ở bài15 (Phía trên).
Đo mỗi góc của ΔABC ta được: ∠A = ∠B = ∠C =600
17. Trên mỗi hình 68,69,70 sau có tam giác nào bằng nhau? Vì sao?
* Hình 68: Ta có: AB = AB(cạnh chung)
AC = AD (gt)
BC = BD (gt)
vậy ∆ABC= ∆ABD(c.c.c)
* Hình 69. Ta có:
∆ MNQ = ∆ QPM (c.c.c)
vì MN = QP (gt)
NQ = PM(gt)
MQ = QM(cạnh chung)
* Hình 70. Ta có:
∆ EHI = ∆IKE (c.c.c) vì
EH = IK (gt)
HI = KE (gt)
EI = IE(gt)
∆ EHK= ∆ IKH(c.c.c) vì
EH = IK (gt)
EK = IH (gt)
Advertisements (Quảng cáo)
HK = KH (cạnh chung)
Luyện tập 1: Giải bài 18, 19, 20, 21 Toán 7 tập 1
18.
Xét bàitoán: “Δ AMB và Δ ANB có MA = MB, NA = NB (h.71). Chứng minh rằng:∠AMN = ∠BMN.”
1) Hãy ghi giả thiết và kết luận
2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bàitoán trên :
a) Do đó Δ AMN= Δ BMN(c.c.c)
b) MN: cạnh chung
MA= MB( Giả thiết)
NA= NB( Giả thiết)
c) Suy ra ∠AMN = ∠BMN (2 góc tương ứng)
d)Δ AMB và Δ ANB có:
HD: 1)Ghi Giả thiết, kết luận:
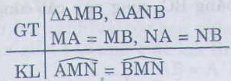2) sắp xếp theo thư tự: d,b,a,c.
Bài 19.
Cho hình 72. Chứng minh rằng:
a) ∆ADE = ∆BDE.
b) ∠ADE = ∠DBE.
Xem hình vẽ ta có:
a) ∆ADE và ∆BDE có:
Advertisements (Quảng cáo)
DE cạnh chung
AD = DB (gt)
AE = BE(gt)
Vậy ∆ADE = ∆BDE(c.c.c)
b) Từ ∆ADE = ∆BDE(Cmt) (Giải thích “cmt”: chứng minh trên)
Suy ra ∠ADE = ∠DBE (Hai góc tương ứng 2 Δ = nhau)
Bài 20 Toán 7.
Cho ∠xOy (h.73), Vẽ cung tròn tâm O, cung tròn này cắt Ox, Oy theo thứ tự ở A,B (1). Vẽ các cung tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong ∠xOy ((2) (3)). Nối O với C (4). Chứng minh OC là tia phân giác của ∠xOy.
HD. xem hình vẽ:
Nối BC, AC.
∆OBC và ∆OAC có:
OB = OA(Bán kính)
BC = AC(gt)
OC cạnh chung
nên ∆OBC = ∆OAC (c.c.c)
Nên ta có ∠BOC = ∠AOC (hai góc tương ứng)
Vậy OC là tia phân giác xOy.
21. Cho ΔABC, Dùng thước và compa, vẽ các tia phân giác của các ∠A,∠B,∠C.
Vẽ tia phân giác của ∠A.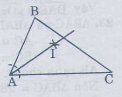
Vẽ cung trong tâm A, cung tròn này cắt AB, AC theo thứ tự ở M,N.
Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong ∠BAC.
Nối AI, ta được AI là tia phân giác của ∠A.
Tương tự cho cách vẽ tia phân giác của các ∠B,∠C (Học sinh tự vẽ).
Luyện tập 2: Bài 22,23 trang 115,116
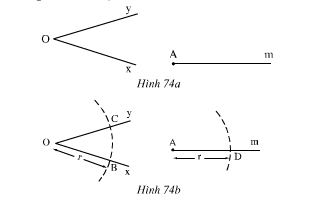
22. Cho ∠xOy và tia Am (h.74a)
Vẽ cung trong tâm O bán kính r, Cung tròn này cắt Ox,Oy theo thứ tự ở B,C. Vẽ cung tròn tâm A bán kính R, cung này cắt kia Am ở D(h.74b).
Vẽ cung tròn tâm D có bán kính bằng BC, cung tròn này cắt cung tròn tam A bán kính r ở E(h. 74c).
Chứng minh rằng ∠DAE = ∠xOy.
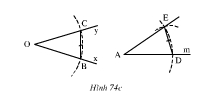
Xét ΔDAE và ΔBOC có:
AD = OB (gt)
DE = BC (gt)
AE = OC (gt)
Nên ∆DAE= ∆BOC (c.c.c)
suy ra ∠DAE = ∠BOC(hai góc tương tứng)
vậy ∠DAE = ∠xOy.
23.Cho đoạn thẳng AB dài 4cm Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm, chúng cắt nhau ở C và D, chứng minh rằng AB là tia phân giác của góc CAD
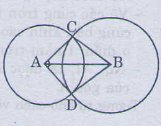
∆BAC và ∆BAD có: AC= AD (gt)
BC = BD(gt)
AB cạnh chung.
Nên ∆BAC= ∆BAD(c.c.c)
Suy ra ∠BAC = ∠BAD (góc tương ứng)
Vậy AB là tia phân giác của ∠CAD.
