Trong bài viết này, Dethikiemtra.com xin giới thiệu Đề thi học kỳ 1 môn Toán lớp 7 của Phòng GD&ĐT Đại Từ – Thái Nguyên.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐẠI TỪ
ĐỀ KIỂM TRA HỌC KÌ I
MÔN TOÁN – LỚP 7
Thời gian làm bài 90 phút không kể thời gian giao đề
A. ĐỀ BÀI
1. (1,5 điểm) Thực hiện phép tính (bằng cách hợp lí nếu có thể)
2. (1,0 điểm) Tìm các số a, b, c biết chúng tỉ lệ với 3; 2; 5 và a – b + c = 12
3. (1,0 điểm) Vẽ đồ thị của hàm số y = 1/2x.
4. (1,5 điểm) Cho biết ba người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (với cùng năng suất như thế) làm cỏ cánh đồng hết bao nhiêu thời gian.
5. (1,5 điểm) Vẽ hình theo cách diễn đạt bằng lời sau:
Vẽ góc xOy có số đo bằng 50o. Lấy điểm A bất kì nằm trong góc xOy. Vẽ qua A đường thẳng d1 vuông góc với Ox tại B, cắt Oy tại D và đường thẳng d2 song song với Ox, cắt Oy tại C.
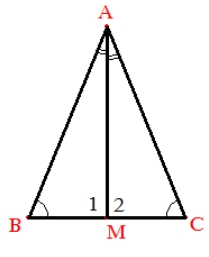
6. (2,5 điểm) Cho tam giác ABC có góc B = góc C, Tia phân giác của góc A cắt BC tại M. Chứng minh rằng:
a) ΔABM = ΔACM
b) AM ⊥ BC
7. (1,0 điểm) So sánh 2600 và 3400
=== HẾT ====
Advertisements (Quảng cáo)
B.ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
CÂU 1. (1,5 ĐIỂM)
2. (1 điểm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Suy ra: a = 3.2 = 6
b = 2.2 = 4
Advertisements (Quảng cáo)
c = 5.2 = 10
Vậy ba số a, b, c lần lượt là 6; 4; 10
3. (1 điểm)
Cho x = 2 thì y = 1 => A(2;1) thuộc đồ thị của hàm số y = 1/2x
Đường thẳng OA là đồ thị của hàm số y = 1/2x
4. (1,5 điểm)
Gọi thời gian để 12 người (cùng năng suất) làm cỏ hết cánh đồng là x (h).
Vì trên cùng một cánh đồng và với năng suất như nhau thì số
người làm cỏ hết cánh đồng đó và số giờ là hai đại lượng tỉ lệ
nghịch, nên ta có: 3.6 = 12.x
Vậy thời gian để 12 người (cùng năng suất) làm cỏ hết cánh
đồng là 1,5 giờ.
5. (1,5 điểm)
6. (2,5 điểm)
Vẽ hình, viết GT, KL đúng.
a) Lập luận được: ∠M1 = ∠M 2 theo định lí
tổng ba góc trong một tam giác
Chứng minh được:
∆ABM = ∆ACM (g.c.g).
b) Vì ∠M1 = ∠M 2 (chứng minh trên)
Mà ∠M1 + ∠ M2 = 180° (Hai góc kề bù)
=> ∠M1 = ∠M2 = 180°/2 = 90°
=> AM ⊥ BC
7. (1 điểm)

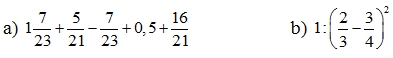

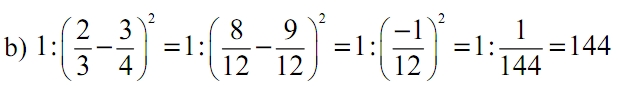
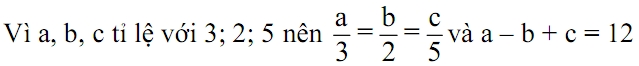






![[Trắc nghiệm + Tự luận] đề thi kiểm tra Toán 7 cuối học kì 2 không thể bỏ lỡ](https://dethikiemtra.com/wp-content/uploads/2018/04/toan-7-100x75.jpg)