Tóm tắt lý thuyết và Giải bài 1 trang 107; Bài 2,3,4,5 trang 108; Bài 6,7,8,9 trang 109 SGK Toán 7 tập 1(Phần luyện tập): Tổng ba góc của một tam giác – Chương 2: Tam giác.
A. Tóm tắt lý thuyết tổng ba góc của một tam giác.
1. Tổng ba góc của một tam giác
Định lí: Tổng ba góc của một tam giác bằng 1800
2. Áp dụng vào tam giác vuông.
Trong tam giác vuông có hai góc nhọn phụ nhau.
3. Góc ngoài của tam giác
a) Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác.
b) Định lí: Mỗi góc ngoài của một tam giác bằng tổng hai góc không kề với nó.
c) Nhận xét: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó.
B. Hướng dẫn giải bài tập: Tổng ba góc của 1 tam giá – sách giáo khoa trang 107,108,109 .
Bài 1. Tính số đo x và y ở các hình 47.48.49,50,51: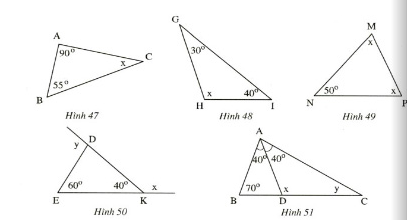
Hình 47:
x+ 900 + 550 = 1800
⇒ x = 1800 – ( 900+ 550)= 350
Hình 48:
x+ 400 + 300 = 1800
⇒ x= 1800 – ( 400+ 390)= 1100
Hình 49:
x+ x + 500= 1800
⇒2x= 1800 – 500 = 1300
⇒ x= 1300 : 2 = 650
Hình 50:
y = 600 + 400= 1000 (Mỗi góc ngoài của một tam giác bằng tổng hai góc không kề với nó)
Ta có: x + 400 = 1800 (kề bù)
⇒x = 1800 – 400 = 1400
Hình 51:
Trong ∆ ABC có
(400+ 400) + 700 + y = 1800
⇒ y + 1500 = 1800
⇒ y = 1800 – 1500= 300
Trong ∆ ACD có:
x + 400 + 300= 1800 ( Góc y = 300 giải được ở trên)
x= 1800 – ( 400+ 300)= 1100
Bài 2 trang 108 SGK Toán 7. Cho tam giác ABC ∠B= 800, ∠C = 300. Tia phân giác của góc A cắt BC ở D. Tính ∠ADC; ∠ADB.
Hình vẽ: 
Gọi A1, A2 là 2 góc được tạo ra bởi tia phân giác góc A.
Ta có:
Góc ∠BAC = 1800 – ( ∠B + ∠C)
Advertisements (Quảng cáo)
= 1800 – ( 800 + 300) = 700
Hay ta có thể gọi ∠A = 700
Góc ∠A1 = ∠A2
= ∠A/2 = 700 /2 = 350
- Xét tam giác ADC ta có: Góc ∠ADC = 1800 – (∠C + ∠A2)
= 1800 – (350 + 300)= 1150
- Do đó góc ∠ADB = 1800 – ∠ADC
= 1800 – 1150
= 650
Bài 3 trang 108 .Cho hình 52. Hãy so sánh: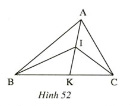 
a) ∠BIK và ∠BAK.
b) ∠BIC và và ∠BAC
Giải: a) Ta có ∠BIK là góc ngoài của ∠BAI( hay là góc ngoài ∠BAK)
Các em lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên ∠BIK > ∠BAK (1)
b) Góc ∠CIK > ∠CAI (2) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: ∠BIK + ∠CIK > ∠BAK + ∠CAI
Mà ∠BIC = ∠BIK + ∠CIK; ∠BAC = ∠BAK + ∠CAI
⇒ ∠BIC > ∠BAC.
Bài 4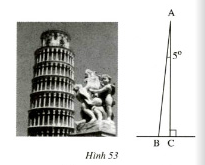 
Đố:Tháp nghiêng Pi – da ở Italia nghiêng 50 so với phương thẳng đứng(h.53). Tính số đo của góc ABC trên hình vẽ.
Ta có: tam giác nghiêng 50 tại A và tam giác ABC là tam giác vuông, vuông ở C. Nên ∠A + ∠B = 900
⇔ 50+ ∠B = 900
⇒ ∠B = 900 – 50 = 850
Vậy số đo góc ABC là: ∠A =50;∠B = 850;∠C= 900
Bài 5 trang 108. Ta gọi tam giác có ba góc nhọn là tam giác nhọn, tam giác có một góc tù là tam giác tù. Gọi tên tam giác nhọn, tam giác tù, tam giác vuông trên hình 54.
Advertisements (Quảng cáo)
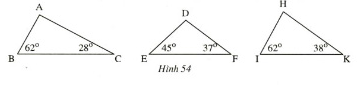
Tam giác vuông ABC ; Tam giác tù DEF; Tam giác nhọn HIK
Giải các bài tập phần Luyện tập Tổng ba góc của một tam giác trang 109 Toán hình học 7
Bài 6. Tìm các số đo x ở các hình sau:
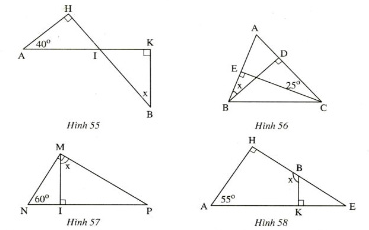
Hình 55:
Ta có ∠A + ∠AIH = 900 (Vì tam giác AHI cân tại H) ⇒∠AIH = 900 – 400 = 500
mà ∠AIH = ∠BIK( 2 góc đối đỉnh) ⇒∠BIK = 500
Ta lại có: ∠IBK +∠BIK = 900 (Vì tam giác IKB cân tại K)
⇒ ∠IBK = 900 – 500 = 400
⇒ x = 400
Hình 56:
Các em có thể giải theo cách của bài 55 tuy nhiên là hơi dài và chúng ta có cách khác làm nhanh hơn. (Áp dụng hình 56 và các hình sau nhé)
Ta có :
Xét tam giác ABD cân tại D ta có ∠ABD + ∠BAD = 900
Xét tam giác ACE cân tại E ta có ∠ACE + ∠EAC = 900
Mà ta có ∠BAD cũng chính là góc ∠EAC
Suy ra ∠ABD = ∠ACE = 250
Vậy ∠ABD = 250 => x = 250
Hình 57:
Xét tam giác MNP vuông tại M ⇒ ∠MNP+ ∠MPN = 900
⇔ 600 + ∠MPN = 900
⇒ ∠MPN = 900 – 600 = 300
Tiếp tục xét tam giác IMP vuông tại I ⇒ ∠IMP + ∠IPM = 900
⇔ ∠IMP + 300 = 900 ( vì∠IPM = ∠MPN )
⇒∠IMP = 900 – 300 = 600
Vậy ∠IMP = 600 => x = 600
Hình 58:
Ta có
Xét tam gác HAE vuông tại H nên ta có ∠HEA = 900 – ∠HAE = 900 – 550 = 350
hay chính là góc ∠BEK = 350
Ta có: ∠HBK = ∠BEK + ∠BKE (Góc ngoài tam giác BKE)
⇒ ∠HBK = 350+ 900 = 1250
Vậy x = 1250
Bài 7 trang 109 Toán 7 tập 1 . Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC(H nằm trên BC).
a) Tìm các cặp góc phụ nhau trong hình vẽ.
b) Tìm các cặp góc nhọn bằng nhau trong hình vẽ.
Vẽ hình:
a) Tam giác ABC vuông tại A nên có ∠B + ∠C = 900
Hay ta có cách gọi khác là ∠B, ∠C phụ nhau
Tam giác AHB vuông tại H nên có ∠B + ∠A1 = 900
hay ∠B , ∠A1 phụ nhau.
Tam giác AHC vuông tại H nên có ∠A2 + ∠C = 900
hay ∠A2 , ∠C phụ nhau.
b) Ta có: ∠B + ∠C = 900
∠B + ∠A1 = 900
⇒∠C = ∠A1
Lại có: ∠B + ∠C = 900
và ∠A2 + ∠C = 900
⇒ ∠B = ∠A2
Bài 8 trang 109. Cho tam giác ABC có ∠B = ∠C= 400. Gọi Ax là tia phân giác của góc ngoài ở đỉnh A, Hãy chứng tỏ Ax//BC.
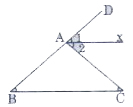
Ta có: ∠CAD = ∠B + ∠C (góc ngoài của tam giác ABC)
= 400+ 400 = 800
∠A2 =1/2 ∠CAD = 800/2 = 400.
=> ∠B = ∠A2 mà hai góc này so le trong với nhau nên Ax// BC.
Bài 9. Hình 59 biểu diễn mặt cắt ngang của một con đê. Để đo góc nhọn MOP tạo bởi mặt phẳng nghiêng của con đê với phương nằm ngang, người ta dùng thước chữ T và đặt như hình vẽ(OA⊥AB). Tính góc MOP, biết rằng dây dọi BC tạo với trụng BA một góc ∠ABC = 320
Ta có tam giác ABC vuông ở A nên ∠ABC + ∠BCA = 900
Trong đó tam giác OCD vuông ở D có ∠COD + ∠OCD = 900
mà góc ∠BCA = ∠OCD ( 2 góc đối đỉnh)
Từ (1),(2),(3) ∠COD = ∠ABC mà ∠ABC= 320 . Nên ∠COD = 320
hay chính là ∠MOP =320
