Câu 77: Thùng của một xe tải có dạng một hình lăng trụ đứng (h.159) các kích thước cho ở trên hình.
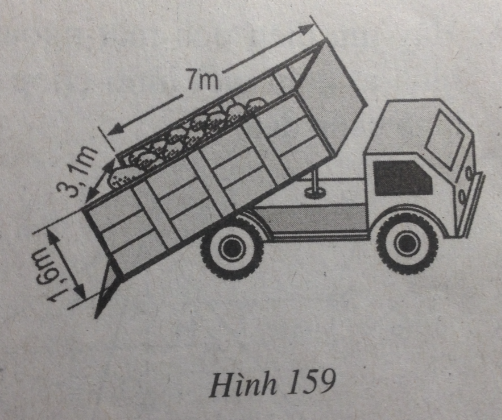
a. Tính thể tích của thùng chứa.
b. Nếu 1m3 cát nặng 1,6 tấn và xe chở đến ${3 \over 4}$ trọng tải của nó thì sức nặng cát lúc đó là bao nhiêu ?
c. Khi cát được san phẳng chở đầy thì phần diện tích của nó bên trong thùng xe là bao nhiêu ?
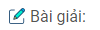
a. Thể tích của thùng chứa bằng: \(V = 3,1.7.1,6 = 34,72({m^3})\)
b. Phần thể tích chở cát bằng: \(34,72.{3 \over 4} = 26,04({m^3})\)
Lượng cát cân nặng là: 26,04.1,6 = 41,664 (tấn)
c. Khi cát san phẳng chở đầy thì diện tích của nó bên trong thùng gồm diện tích xung quanh của hình hộp chữ nhật có kích thước là 3,1m; 7m và 1,6m cùng với đáy hình chữ nhật kích thước bằng 3,1m và 7m.
Diện tích cát bên trong thùng là:
\(2.\left( {7 + 3,1} \right).1,6 + 3,1.7 = 54,02({m^2})\)
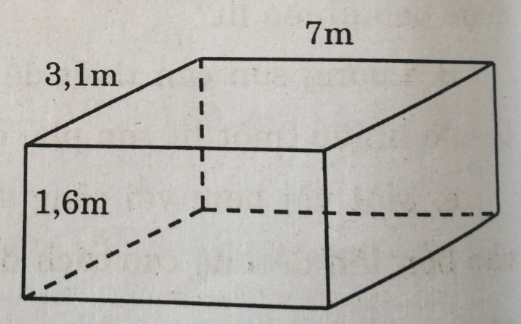
Câu 78: Độ dài đường chéo AC1 (h.160) của một hình lập phương là \(\sqrt {12} \) .
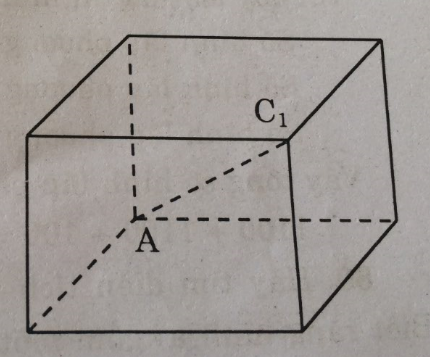
a. Độ dài mỗi cạnh là bao nhiêu ?
b. Tính diện tích toàn phần và thể tích
của hình lập phương.
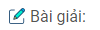
(hình 160 trang 155 sbt)
Advertisements (Quảng cáo)
a. Gọi a là độ dài của hình lập phương. Vì là hình lập phương nên kích thước các cạnh bằng nhau.
Như vậy đường chéo đáy là đường chéo hình vuông cạnh a.
Độ dài đường chéo đáy là \(a\sqrt 2 \)
Suy ra:
\(\eqalign{ & A{C_1}^2 = {\left( {a\sqrt 2 } \right)^2} + {a^2} \cr & = 2{a^2} + {a^2} = 3{a^2} \cr} \)
Mà \(A{C_1} = \sqrt {12} \) nên \(3{a^2} = 12 \Rightarrow {a^2} = 4 \Rightarrow a = 2\)
Vậy cạnh hình lập phương bằng 2 (đơn vị dài)
b. Diện tích toàn phần hình lập phương:
\({S_{TP}} = 6.\left( {2.2} \right) = 24\) (đơn vị diện tích)
Thể tích hình lập phương:
V = 2.2.2 = 8 (đơn vị thể tích)
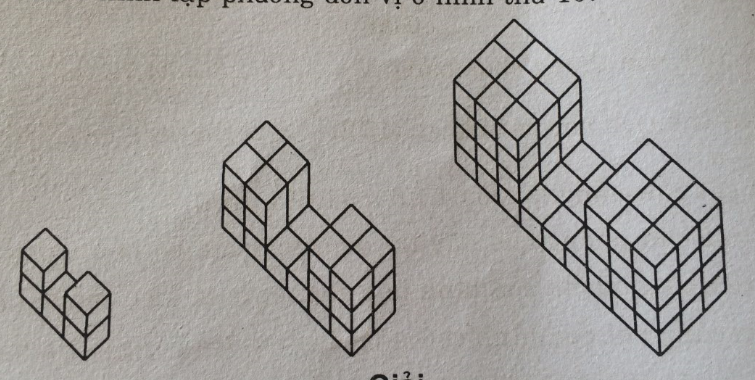
Câu 79: Hãy quan sát ba hình dưới đây (h.161), trong đó có các hình lập phương đơn vị được xếp theo dạng chữ U.
Advertisements (Quảng cáo)
Số các hình lập phương đã xếp tăng lên theo quy luật 5 hình → 28 hình → 81 hình.
Nếu theo quy luật này thì có bao nhiêu hình lập phương đơn vị ở hình thứ 10 ?
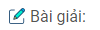
(hình 161 trang 155 sbt)
Khi vẽ hình thứ 3, ta có:
Số hình lập phương đơn vị bên trái là 3.4.3 = 36
Số hình lập phương đơn vị bên phải là 3.4.3 = 36
Số hình lập phương đơn vị ở giữa: 3.3 = 9
Vậy có tổng số: 36 + 36 + 9 = 81 hình lập phương đơn vị.
Với quy luật đó thì hình thứ 10:
Số hình lập phương đơn vị bên trái: 10.11.10 = 1100
Số hình lập phương đơn vị bên phải: 10.11.10 = 1100
Số hình lập phương đơn vị ở giữa: 10.10 = 100
Vậy tổng số hình lập phương đơn vị của hình thứ 10 là:
1100 + 1100 + 100 = 2300 hình
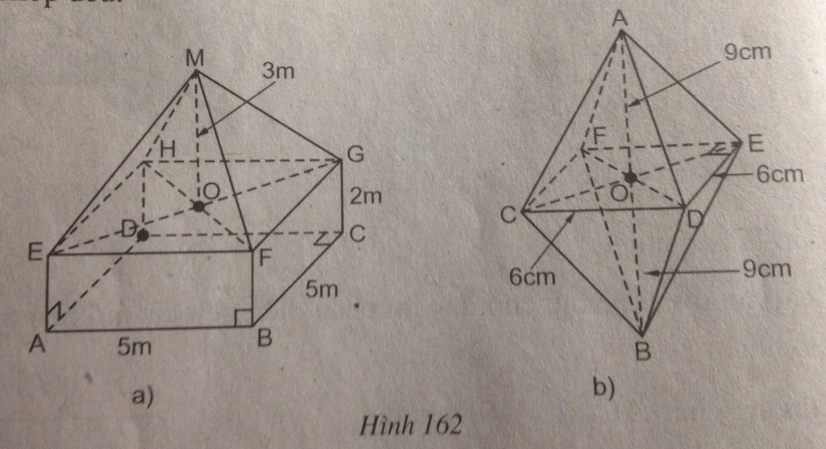
Câu 80: Hãy tìm diện tích mặt ngoài theo các kích thước cho ở hình 162. Biết rằng hình a gồm một hình chóp đều và một hình hộp chữ nhật, hình b gồm hai hình chóp đều.
(hình 162 trang 156 sbt)
Hình a:
Diện tích xung quanh hình hộp chữ nhật là:
\({S_{xq}} = 4.5.2 = 40(c{m^2})\)
Diện tích đáy hình hộp chữ nhật là:
\(S = 5.5 = 25(c{m^2})\)
Đường cao hình chóp bằng 3 nên đường cao mặt bên bằng:
\(\sqrt {{3^2} + {{\left( {2,5} \right)}^2}} = \sqrt {9 + 6,25} = \sqrt {15,25} \approx 3,9(cm)\)
Diện tích xung quanh hình chóp đều:
\({S_{xq}} = {1 \over 2}.\left( {5.4} \right).3,9 \approx 39(c{m^2})\)
Vậy diện tích xung quanh vật thể bằng:
\(40 + 25 + 39 = 104(c{m^2})\)

