Câu 70: Tính thể tích và diện tích toàn phần các hình chóp đều dưới đây (theo các kích thước cho trên hình vẽ 153).
(xem hình 153)
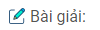
(hình 153 trang 153 sbt)
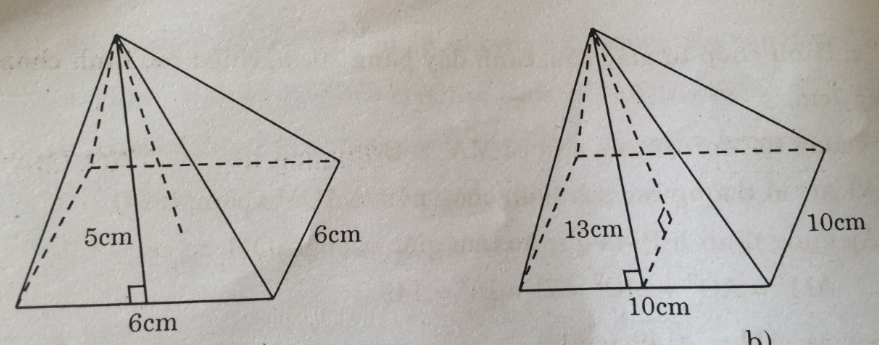
– Hình a:
Đường cao hình chóp bằng: \(\sqrt {{5^2} – {3^2}} = \sqrt {25 – 9} = \sqrt {16} = 4(cm)\)
Diện tích đáy bằng: \(S = 6.6 = 36(c{m^2})\)
Thể tích hình chóp bằng: \(V = {1 \over 3}S.h = {1 \over 3}.36.4 = 48(c{m^3})\)
Diện tích xung quanh bằng: \({S_{xq}} = Pd = 2.6.5 = 60(c{m^2})\)
Diện tích toàn phần là: STP = Sxq + Sđáy = 60 + 36 = 96 (cm2)
– Hình b:
Đường cao hình chóp bằng: \(\sqrt {{{13}^2} – {5^2}} = \sqrt {144} = 12(cm)\)
Diện tích đáy của hình chóp bằng: S = 10.10 = 100 (cm2)
Thể tích hình chóp bằng: \(V = {1 \over 3}S.h = {1 \over 3}.100.12 = 400(c{m^3})\)
Diện tích xung quanh hình chóp bằng:
\({S_{xq}} = Pd = 10.2.13 = 260(c{m^2})\)
Diện tích toàn phần của hình chóp bằng:
STP = Sxq + Sđáy = 260 + 100 = 360 (cm2)
Advertisements (Quảng cáo)
Câu 71: Tính diện tích toàn phần của hình chóp cụt đều cho theo các kích thước trên hình 154.
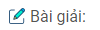
(hình 154 trang 153 sbt)
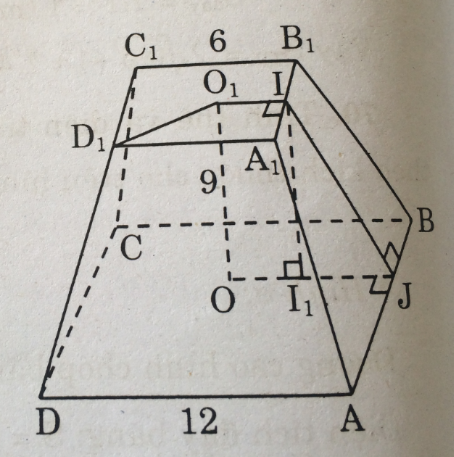
Ta có: A1D1 = 6 \( \Rightarrow {O_1}I = 3\)
\(AD = 12 \Rightarrow {\rm O}J = 6\)
Kẻ II1 ⊥ OJ, ta có: I1J = 3
Áp dụng định lí Pi-ta-go vào tam giác vuông II1J, ta có:
\(I{J^2} = I{I_1}^2 + {I_1}{J^2} = {9^2} + {3^2} = 90\)
Suy ra:
Diện tích mặt một bên là một hình thang bằng:
\(S = {1 \over 2}\left( {6 + 12} \right).\sqrt {90} = 9\sqrt {90} \) (đvdt)
Advertisements (Quảng cáo)
Diện tích xung quanh bằng : Sxq = \(4.9.\sqrt {90} = 36\sqrt {90} \) (đvdt)
Diện tích đáy trên bằng: S = 6.6 = 36 (đvdt)
Diện tích đáy dưới bằng: S = 12.12 = 144 (đvdt)
Diện tích toàn phần của hình chóp cụt là:
\({S_{TP}} = 36\sqrt {90} + 36 + 144 = \left( {36\sqrt {90} + 180} \right)\) (đvdt)
Câu 72
Cho hình chóp cụt tứ giác đều ABCD.A1B1C1D1 có các cạnh đáy 5cm và 10cm, đường cao của mặt bên bằng 5cm. Hãy tính:
a. Diện tích xung quanh của hình chóp cụt.
b. Tính cạnh bên và chiều cao của hình chóp cụt.
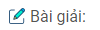
(hình trang 163 sgbt)
a. Diện tích một mặt bên là hình thang bằng :
\(S = {1 \over 2}\left( {5 + 10} \right).5 = 37,5(c{m^2})\)
Diện tích xung quanh của hình chóp cụt đều là:
\({S_{xq}} = 4.37,5 = 150(c{m^2})\)
b. Kẻ A1H ⊥ AB, ta có:
A1I = 2,5cm; AJ = 5cm
Suy ra: AH = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông A1HA, ta có:
\({A_1}{A^2} = {A_1}{H^2} + A{H^2} = {5^2} + 2,{5^2} = 31,25\)
Suy ra: \({A_1}A = \sqrt {31,25} \approx 5,59(cm)\)
Ta có: \({O_1}I = 2,5cm;OJ = 5cm.\)
Kẻ II1 ⊥ OJ, suy ra I1J = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông II1J, ta có:
\(I{J^2} = I{I_1}^2 + {{\rm I}_1}{J^2}\)
Suy ra: \(I{I_1}^2 = I{J^2} – {I_1}{J^2} = {5^2} – 2,{5^2} = 18,75\)
Suy ra: \(I{I_1} = \sqrt {18,75} \approx 4,33(cm)\)
Vậy O1O = II1 = 4,33 (cm)

