Câu 20: Từ một tờ giấy hình vuông kích thước 3 × 3 liệu có thể gấp để tạo thành một hình lập phương đơn vị hay không ? (có thể làm nắp rời)
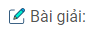
(hình trang 133 sgbt)
Triển khai hình lập phương không có nắp ta được 1 hình chữ thập gồm 2 hình chữ nhật có chiều rộng 1 ( đơn vị dài ) và chiều dài 3 ( đơn vị dài )
Sắp xếp như hình vẽ, ta có tam giác vuông cân ở góc nhỏ có cạnh huyền 1 đơn vị dài thì cạnh góc vuông là \({{\sqrt 2 } \over 2}\) ( đơn vị dài )
Tam giác vuông cân có cạnh huyền là 3 đơn vị dài thì cạnh góc vuông bằng \({{3\sqrt 2 } \over 2}\) đơn vị dài.
Khi đó tổng độ dài là \({{3\sqrt 2 } \over 2} + {{\sqrt 2 } \over 2} = 2\sqrt 2 \) đơn vị dài < 3
Vậy hình chữ thập đó đặt gọn trong tờ giấy có kích thước 3×3
Phần thừa ở 4 góc là 4 tam giác vuông đủ để làm nắp
Vậy có thể gấp được hình lập phương đơn vị từ tờ giấy 3×3
Advertisements (Quảng cáo)
Câu 21: Tìm trên hình hộp chữ nhật ABCD.A1B1C1D1 (h.113) một ví dụ cụ thể để chứng tỏ mệnh đề sau là sai:
Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
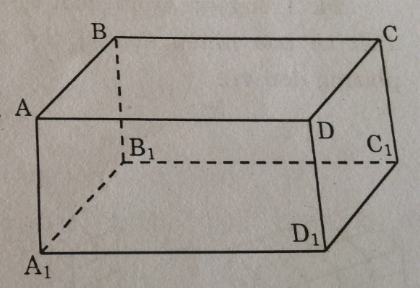
(hình 113 trang 136 sbt)
Ta có: AB ⊥ BC
Advertisements (Quảng cáo)
CC1 ⊥ BC
Nhưng AB và CC1 không song song với nhau.
Vậy mệnh đề đã cho là sai
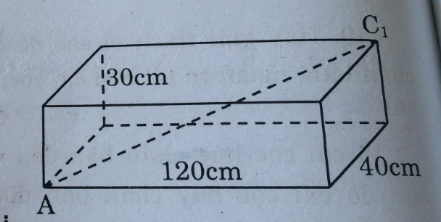
Câu 22: Các kích thước của một hình hộp chữ nhật như ở hình 114, độ dài đoạn AC1 là:
A. 190cm
B. 150cm
C. 130cm
D. 109cm
Hãy chọn kết quả đúng.
Áp dụng định lí Pi-ta-go, ta tính được:
– Đường chéo của mặt đáy bình phương bằng: \({40^2} + {120^2}\)
– Đường chéo của mặt chéo bình phương bằng: \({40^2} + {120^2} + {30^2}\)
Suy ra: \(A{C_1} = \sqrt {{{40}^2} + {{120}^2} + {{30}^2}} = 130\)
Vậy chọn đáp án C

