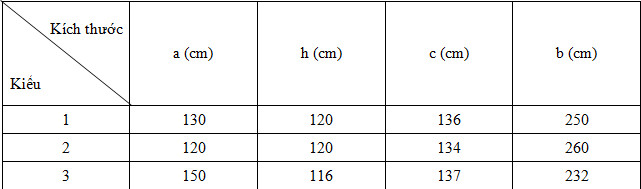
Câu 40: Hình 129 là một cái lều ở trại hè, có dạng một lăng trụ đứng kèm theo các kích thước (xem bảng).
(xem hình 129)
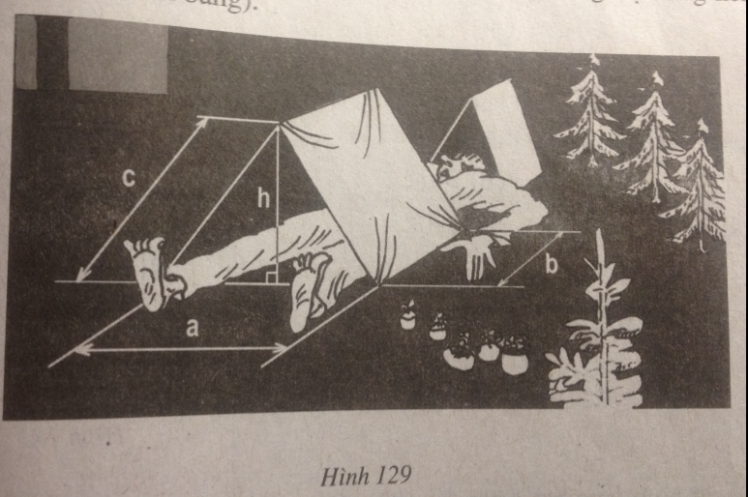
Sau đây là ba kiểu để học sinh lựa chọn
a. Với mỗi kiểu, hãy tính thể tích của lều.
b. Tính phần diện tích của lều nhận được ánh sáng từ Mặt Trời (phần này gồm hai hình chữ nhật và hai tam giác).
c. Với yêu cầu nói trên, nên chọn kiều lều nào để thể tích của lều lớn nhất ?
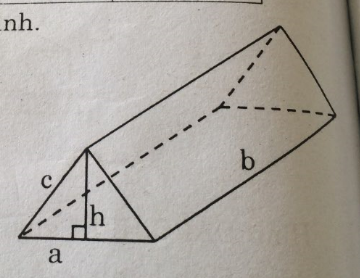
a. Ta có thể xem cái lều là một lăng trụ đứng đáy tam giác cân cạnh bên bằng c, cạnh đáy bằng a, đường cao đáy là h, đường cao hình lăng trụ là b.
Áp dụng công thức: V = S.h, ta có:
– Kiểu 1:
\(\eqalign{ & S = {1 \over 2}.130.120 = 7800(c{m^2}) \cr & V = 7800.250 = 1950000(c{m^3}) \cr} \)
– Kiểu 2:
\(\eqalign{ & S = {1 \over 2}.120.120 = 7200(c{m^2}) \cr & V = 7200.260 = 1872000(c{m^3}) \cr} \)
– Kiểu 3:
\(\eqalign{ & S = {1 \over 2}.150.116 = 8700(c{m^2}) \cr & V = 8700.232 = 2018400(c{m^3}) \cr} \)
b. Hai mặt bên là hai hình chữ nhật bằng nhau có kích thước là c và b, có diện tích:
– Kiểu 1: Diện tích hai mặt bên là: \(2\left( {136.250} \right) = 68000(c{m^2})\)
Advertisements (Quảng cáo)
Phần diện tích lều được nhận ánh sáng là:
\(7800.2 + 68000 = 83600(c{m^2})\)
– Kiểu 2: Diện tích hai mặt bên là: \(2\left( {134.260} \right) = 69680(c{m^2})\)
Phần diện tích lều được nhận ánh sáng là:
\(7200.2 + 69680 = 84080(c{m^2})\)
– Kiểu 3: Diện tích hai mặt bên là: \(2\left( {137.232} \right) = 63568(c{m^2})\)
Phần diện tích lều được nhận ánh sáng là:
\(8700.2 + 63568 = 80968(c{m^2})\)
c. Vậy chọn kiểu 3 thì thể tích lều lớn nhất.
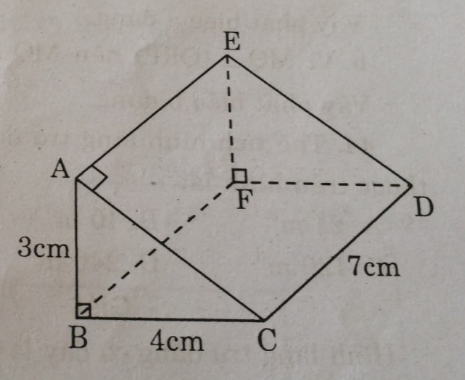
Câu 41: Tìm diện tích toàn phần của hình lăng trụ đứng (theo kích thước đã cho trên hình 130).
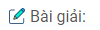
Advertisements (Quảng cáo)
(hình 130 trang 144 sbt)
Áp dụng định lí Pi-ta-go vào tam giác vuông BAC, ta có:
\(\eqalign{ & A{C^2} = B{A^2} + B{C^2} \cr & = {3^2} + {4^2} = 25 \cr & AC = 5(m) \cr} \)
Diện tích xung quanh là:
\(\eqalign{ & {S_{xq}} = \left( {AB + BC + AC} \right).CD \cr & = \left( {3 + 4 + 5} \right).7 = 84({m^2}) \cr} \)
Diện tích đáy là: Sđáy = \({1 \over 2}.BA.BC = {1 \over 2}.3.4 = 6({m^2})\)
Diện tích toàn phần là: STP = S xq + 2.Sđáy = 84 + 2.6 = 96 (m2)
Câu 42: Diện tích toàn phần của hình lăng trụ đứng, tính theo các kích thước đã cho trên hình 131 là:
(xem hình 131)
A. 228
B. 240
C. 196
D. 170
E. 210.
Hãy chọn kết quả đúng.
Dựa vào số đo các cạnh hình lăng trụ, lần lượt tính diện tích các mặt bên và hai đáy. Ta có diện tích toàn phần của hình lăng trụ đứng là 228.
Vậy chọn đáp án A.
Câu 43: Quan sát hình lăng trụ đứng (h.132).
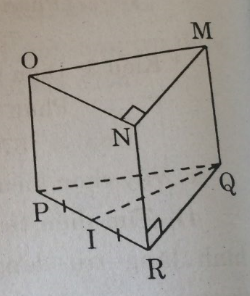
Các phát biểu sau đây đúng hay sai ?
a. Các cạnh QM và MO vuông góc với nhau.
b. MQ vuông góc với QI (I là trung điểm của PR).
Ta có hình lăng trụ đứng MNO.QRP.
a. Vì mặt bên (MOPQ) là một hình chữ nhật nên
MQ ⊥ MO.
Vậy phát biểu a đúng.
b. Vì MQ ⊥ (QRP) nên MQ ⊥ QI
Vậy phát biểu b đúng.

