Câu 48: Lăng trụ đứng có kích thước như ở hình 137 thì thể tích của nó là:
A. 390cm3
B. 360cm3
C. 450cm3
D. 420cm3
E. 410cm3
Hãy chọn kết quả đúng.


(hình 137 trang 146 sbt)
Lăng trụ đứng có đáy là tam giác vuông với hai cạnh góc vuông là 5cm và 12cm, đường cao lăng trụ bằng 15cm.
Ta có: \(V = S.h = {1 \over 2}.5.12.15 = 450(c{m^3})\)
Vậy chọn đáp án C.
Câu 49: Theo các kích thước của hình lăng trụ đứng đáy tam giác cho trên hình 138 thì trong các số sau:
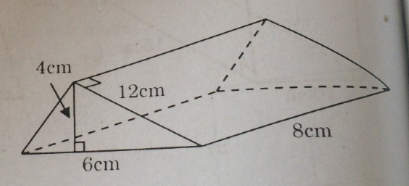
A. 48cm3
B. 96cm3
C. 192cm3
D. 384cm3
số nào là thể tích của nó ?
Advertisements (Quảng cáo)
Hãy chọn kết quả đúng.

Lăng trụ đứng có đáy là tam giác cân với cạnh đáy là 6cm, đường cao đáy 4cm, đường cao lăng trụ là 8cm.
Ta có: \(V = S.h = {1 \over 2}.6.4.8 = 96(c{m^3})\)
Vậy chọn đáp án B.
Câu 50: Một nhà kho có dạng một lăng trụ đứng như hình 139 với BC = ED = CD = 10 (m) và DH = 20 (m), AB = AE. Chiều cao từ đỉnh A đến nền nhà là 15 (m).

Thể tích nhà kho là (m3)
A. 1800
B. 2000
C. 2500
D. 2200
Advertisements (Quảng cáo)
E. 1600
Hãy chọn kết quả đúng.

Chia nhà kho thành hai phần gồm lăng trụ đứng đáy hình tam giác cân ABE.KFG có cạnh đáy BE = CD = 10m, đường cao đáy bằng AM – BC = 15 – 10 = 5m, đường cao lăng trụ là 20m và hình hộp chữ nhật với đáy có kích thước 10m và 15m, chiều cao bằng 10m.
Thể tích lăng trụ là : \(V = S.h = {1 \over 2}.10.5.20 = 500(c{m^3})\)
Thể tích của hình hộp chữ nhật là: \(V = 10.20.10 = 2000({m^3})\)
Thể tích của kho là: \(500 + 2000 = 2500({m^3})\)
Vậy chọn đáp án C.
Câu 51: Tính thể tích và diện tích toàn phần của các hình lăng trụ đứng có các kích thước như trên hình 140.
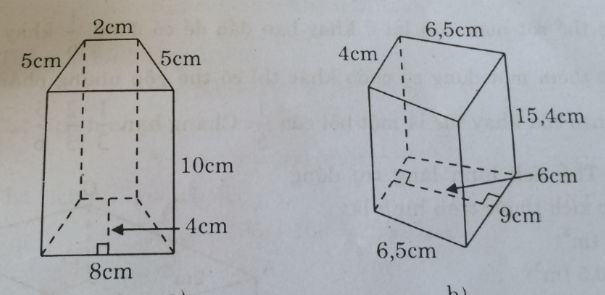

(hình 140 trang 147 sbt)
– Hình a:
Diện tích xung quanh bằng:
\({S_{xq}} = \left( {5 + 2 + 5 + 8} \right).10 = 200(c{m^2})\)
Diện tích đáy bằng:
Sđáy \( = {{\left( {2 + 8} \right)} \over 2}.4 = 20(c{m^2})\)
Diện tích toàn phần bằng:
STP = Sxq + 2.Sđáy \( = 200 + 2.20 = 240(c{m^2})\)
Thể tích lăng trụ đứng:
\(V = S.h = 20.10 = 200(c{m^3})\)
– Hình b:
Diện tích xung quanh bằng:
\({S_{xq}} = \left( {4 + 6,5 + 9 + 6,5} \right).15,4 = 400,4(c{m^2})\)
Diện tích đáy bằng:
Sđáy \( = {{4 + 9} \over 2}.6 = 39(c{m^2})\)
Diện tích toàn phần bằng:
STP = Sxq + 2.Sđáy \( = 400,4 + 2.39 = 478,4(c{m^2})\)
Thể tích lăng trụ đứng:
\(V = S.h = 39.15,4 = 600,6(c{m^3})\)

