Bài 21: Cho tam giác vuông cân \(OAB\) với \(OA = OB = a\). Hãy dựng các vec tơ sau đây và tính độ dài của chúng.



Vẽ hình vuông OACB, ta có

Gọi \(M, N\) là điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow {OA} ,\,\overrightarrow {ON} = 4\overrightarrow {OB} \).
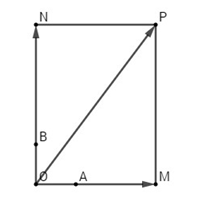
Vẽ hình chữ nhật MONP, ta có

Tương tự, ta cũng có
Advertisements (Quảng cáo)
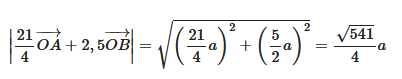

Gọi \(I, J\) là điểm thỏa mãn
\(\overrightarrow {OI} = {{11} \over 4}\overrightarrow {OA} ,\,\overrightarrow {OJ} = – {3 \over 7}\overrightarrow {OB} \)
Vẽ hình chữ nhật OIKJ, ta có

Bài 22: Cho tam giác \(OAB\). Gọi \(M, N\) lần lượt là trung điểm hai cạnh \(OA\) và \(OB\). Hãy tìm các số \(m\) và \(n\) thích hợp trong mỗi đẳng thức sau đây:

Advertisements (Quảng cáo)


Ta có

Bài 23: Gọi \(M\) và \(N\) lần lượt là trung điểm các đoạn thẳng \(AB\) và \(CD\). Chứng minh rằng
\(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} .\)

Theo quy tắc ba điểm, ta có

Bài 24: Cho tam giác \(ABC\) và điểm \(G\). Chứng minh rằng
a) Nếu \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) thì \(G\) là trọng tâm tam giác \(ABC\);
b) Nếu có điểm \(O\) sao cho \(\overrightarrow {OG} = {1 \over 3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) thì \(G\) là trọng tâm tam giác \(ABC\).

a) Gọi \({G_1}\) là trọng tâm tam giác \(ABC\). Từ đó, ta có \(\overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} = \overrightarrow 0 .\)
Theo giả thiết, \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

b) Gọi \( {G_1}\) là trọng tâm tam giác \(ABC\). Từ đó, ta có \(\overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} = \overrightarrow 0 .\)


