Bài 7: Cho sáu điểm \(A, B, C, D, E, F\). Đẳng thức nào dưới đây đúng ?
(A) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} + \overrightarrow {BC} + \overrightarrow {EF} + \overrightarrow {DE} = \overrightarrow 0 \) ;
(B) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} + \overrightarrow {BC} + \overrightarrow {EF} + \overrightarrow {DE} = \overrightarrow {AF} \) ;
(C) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} + \overrightarrow {BC} + \overrightarrow {EF} + \overrightarrow {DE} = \overrightarrow {AE} \) ;
(D) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} + \overrightarrow {BC} + \overrightarrow {EF} + \overrightarrow {DE} = \overrightarrow {AD} \).

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} + \overrightarrow {BC} + \overrightarrow {EF} + \overrightarrow {DE} \)
\(= \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} + \overrightarrow {EF} + \overrightarrow {FA} \)
\(=\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0. \)
Chọn (A).
Advertisements (Quảng cáo)
Bài 8: Cho hình thang \(ABCD\) với hai cạnh đáy là \(AB = 3a\) và \(CD = 6a\). Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {CD} } \right|\) bằng bao nhiêu ?
(A) \(9a\) ; (B) \(3a\) ;
(C) \(-3a\) ; (D) \(0\).

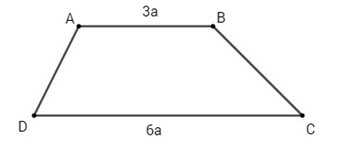
Gọi \(E\) là trung điểm \(CD\). Ta có \(\left| {\overrightarrow {AB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {DE} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CE} } \right| = CE = 3a\).
Advertisements (Quảng cáo)
Chọn (B).
Bài 9: Cho hình vuông \(ABCD\) có cạnh bằng \(a\). Khi đó giá trị \(\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|\) bằng bao nhiêu ?
(A) \(2a\sqrt 2 \); (B) \(2a\);
(C) \(a\); (D) \(0\).

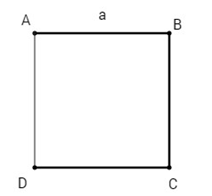
\(\eqalign{
& \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AD} – \overrightarrow {AB} = 2\overrightarrow {AD} \cr
& \Rightarrow \,\,\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right| = \left| {2\overrightarrow {AD} } \right| = 2a. \cr} \)
Chọn (B).
Bài 10: Cho ba điểm bất kì \(A, B, C\). Đẳng thức nào dưới đây đúng ?
(A) \(\overrightarrow {AB} = \overrightarrow {CB} – \overrightarrow {CA} \) ;
(B) \(\overrightarrow {BC} = \overrightarrow {AB} – \overrightarrow {AC} \);
(C) \(\overrightarrow {AC} – \overrightarrow {CB} = \overrightarrow {BA} \);
(D) \(\overrightarrow {CA} – \overrightarrow {CB} = \overrightarrow {AB} \);

Chọn (A).

