Bài 10: Cho hình bình hành \(ABCD\) với tâm \(O\). Hãy điền vào chỗ trống (…) để được đẳng thức đúng
a) \(\overrightarrow {AB} + \overrightarrow {AD} = …………\)
b) \(\overrightarrow {AB} + \overrightarrow {CD} = …………\)
c) \(\overrightarrow {AB} + \overrightarrow {OA} = …………\)
d) \(\overrightarrow {OA} + \overrightarrow {OC} = …………\)
e ) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = …………\)

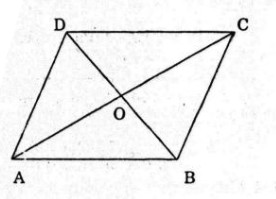
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành).
b) \(\overrightarrow {AB} + \overrightarrow {CD} = \,\overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow 0 \,\)
c) \(\overrightarrow {AB} + \overrightarrow {OA} = \overrightarrow {AB} + \overrightarrow {OB} + \overrightarrow {BA} = \overrightarrow {OB} \) (quy tắc ba điểm).
d) \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) (vì O là trung điểm của AC).
e) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} ) = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \) (vì O là trung điểm của AC).
Bài 11: Cho hình bình hành \(ABCD\) với tâm \(O\). Mỗi khẳng định sau đây đúng hay sai ?
a) \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BD} } \right|\);
b) \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {BC} \);
c) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \);
Advertisements (Quảng cáo)
d) \(\overrightarrow {BD} + \overrightarrow {AC} = \overrightarrow {AD} + \overrightarrow {BC} \).

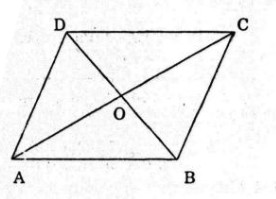
a) Sai vì \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|\) thì chưa chắc \(AC, BD\) đã bằng nhau do \(ABCD\) là hình bình hành.
b) Đúng vì \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \)
c) Sai vì \(\overrightarrow {OA} + \overrightarrow {OB} = \left( {\overrightarrow {OC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {OD} + \overrightarrow {DB} } \right) = \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {CA} + \overrightarrow {DB} } \right) \ne \overrightarrow {OC} + \overrightarrow {OD} \)
d) Đúng vì \(\overrightarrow {BD} + \overrightarrow {AC} = \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) = \left( {\overrightarrow {DC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {AD} } \right) = \overrightarrow {AD} + \overrightarrow {BC} \).
Bài 12: Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\).
a) Hãy xác định các điểm \(M, N, P\) sao cho
\(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \,;\,\,\,\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \,;\,\,\,\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \)
b) Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \).
Advertisements (Quảng cáo)

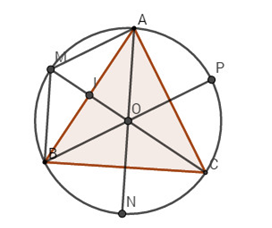
a) Theo quy tắc hình bình hành, ta có \(AOBM\) là hình bình hành.
Ta có \(AB, OM\) cắt nhau tại trung điểm mỗi đường, gọi \(I\) là trung điểm \(AB\) thì \(OI = IM\). \(O\) là trọng tâm tam giác \(ABC\) nên \(OC = 2 OI = OM\).
Do đó \(O\) là trung điểm của \(MC\), tức là \(MC\) là đường kính của đường tròn.
Vậy điểm \(M\) là điểm sao cho \(CM\) là đường kính của đường tròn tâm \(O\).
Tương tự, ta cũng có \(N, P\) thuộc đường tròn \((O)\) sao cho \(AN, BP\) là đường kính của đường tròn \((O)\).
b) \(O\) là trung điểm của \(MC\) nên \(\overrightarrow {OM} + \overrightarrow {OC} = \overrightarrow 0 \), mà \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \)
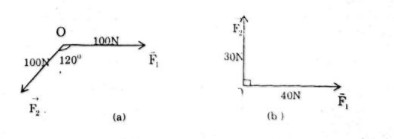
Bài 13: Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt tại \(O\) (h.17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau
a) \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều có cường độ là \(100N\), góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({120^0}\) (h.17a);
b) Cường độ của \(\overrightarrow {{F_1}} \) là \(40N\), của \(\overrightarrow {{F_2}} \) là \(30N\) và góc giữa \(\overrightarrow {{F_1}} \) và \( \overrightarrow {{F_2}} \) bằng (h.17b).

a)
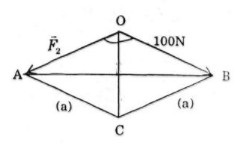
Ta lấy \(\overrightarrow {{F_2}} = \overrightarrow {OA} ,\,\overrightarrow {{F_1}} = \overrightarrow {OB} \).
Theo quy tắc hình bình hành, ta vẽ hình bình hành \(OACB\).
Hình bình hành \(OACB\) có \(OA = OB\) nên \(OACB\) là hình thoi.
Ta có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \), \(OC\) là phân giác góc \(\widehat {AOB}\) nên \(\widehat {AOC} = {60^0}\). Mà \(OACB\) là hình thoi nên tam giác \(AOC\) đều. Suy ra \(OA = OC\). Vậy cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(100N\).
b)
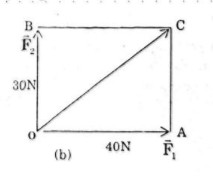
Đặt \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} \). \(C\) là đỉnh thứ tư của hình bình hành \(OABC\).
Do góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({90^0}\) suy ra tứ giác \(OABC\) là hình chữ nhật.
\( \Rightarrow OC = \sqrt {O{A^2} + O{B^2}} = \sqrt {{{40}^2} + {{30}^2}} = 50N\)
Ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Vậy cường độ tổng hợp lực của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(50N.\)

