Bài 14: a) Vectơ đối của vectơ \( – \overrightarrow a \) là vectơ nào?
b) Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ nào?
c) Vectơ đối của vectơ \(\overrightarrow a + \overrightarrow b \) là vectơ nào?

a) Vectơ đối của vectơ \( – \overrightarrow a \) là vectơ \( – ( – \overrightarrow a ) = \overrightarrow a \).
b) Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ \(\overrightarrow 0 \).
c) Vectơ đối của vectơ \(\overrightarrow a + \overrightarrow b \) là vectơ \( – \left( {\overrightarrow a + \overrightarrow b } \right) = – \overrightarrow a – \overrightarrow b \)
Bài 15: Chứng minh các mệnh đề sau đây
a) Nếu \(\overrightarrow a + \overrightarrow b = \overrightarrow c \) thì \(\overrightarrow a = \overrightarrow c – \overrightarrow b ,\overrightarrow b = \overrightarrow c – \overrightarrow a \);
b) \(\overrightarrow a – (\overrightarrow b + \overrightarrow c ) = \overrightarrow a – \overrightarrow b – \overrightarrow c \);
c) \(\overrightarrow a – (\overrightarrow b – \overrightarrow c ) = \overrightarrow a – \overrightarrow b + \overrightarrow c \).

a) Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow b \) ta có
Advertisements (Quảng cáo)
\(\overrightarrow a + \overrightarrow b + \left( { – \overrightarrow b } \right) = \overrightarrow c + \left( { – \overrightarrow b } \right)\,\, \Rightarrow \overrightarrow a = \overrightarrow c – \overrightarrow b \)
Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow a \) ta có
\(\overrightarrow a + \overrightarrow b + \left( { – \overrightarrow a } \right) = \overrightarrow c + \left( { – \overrightarrow a } \right)\,\, \Rightarrow \overrightarrow b = \overrightarrow c – \overrightarrow a \)
b) Ta có \(\overrightarrow a – (\overrightarrow b + \overrightarrow c ) + (\overrightarrow b + \overrightarrow c ) = \overrightarrow a \)
Áp dụng câu a) ta có \(\overrightarrow a – (\overrightarrow b + \overrightarrow c ) = \overrightarrow a – \overrightarrow b – \overrightarrow c \)
c) Áp dụng câu a) ta có \(\overrightarrow a – (\overrightarrow b – \overrightarrow c ) = \overrightarrow a – \left[ {\overrightarrow b + \left( { – \overrightarrow c } \right)} \right] = \overrightarrow a – \overrightarrow b – \left( { – \overrightarrow c } \right) = \overrightarrow a – \overrightarrow b + \overrightarrow c \)
Bài 16: Cho hình bình hành \(ABCD\) với tâm \(O\). Mỗi khẳng định sau đây đúng hay sai ?
a) \(\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {AB} \);
Advertisements (Quảng cáo)
b) \(\overrightarrow {CO} – \overrightarrow {OB} = \overrightarrow {BA} \);
c) \(\overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {AC} \);
d) \(\overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {BD} \);
e) \(\overrightarrow {CD} – \overrightarrow {CO} = \overrightarrow {BD} – \overrightarrow {BO} \).

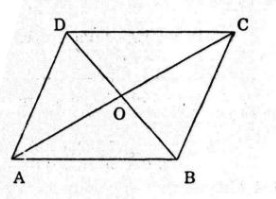
a) Sai vì \(\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {BA} \ne \overrightarrow {AB} .\)
b) Đúng vì \(\overrightarrow {CO} – \overrightarrow {OB} = \overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {BA} .\)
c) Sai vì \(\overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {DB} \ne \overrightarrow {AC} \).
d) Sai vì \(\overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {DB} \ne \overrightarrow {BD} \).
e) Đúng vì \(\overrightarrow {CD} – \overrightarrow {CO} = \overrightarrow {BD} – \overrightarrow {BO} = \overrightarrow {OD} \).
Bài 17: Cho hai điểm \(A, B\) phân biệt.
a) Tìm tập hợp các điểm \(O\) sao cho \(\overrightarrow {OA} = \overrightarrow {OB} \);
b) Tìm tập hợp các điểm \(O\) sao cho \(\overrightarrow {OA} = – \overrightarrow {OB} \).

a) \(\overrightarrow {OA} = \overrightarrow {OB} \) thì \(A = B\) ( vô lý do \(A, B\)) phân biệt).
Vậy tập hợp điểm \(O\) thỏa mãn \(\overrightarrow {OA} = \overrightarrow {OB} \) là tập rỗng.
b) Ta có \(\overrightarrow {OA} = – \overrightarrow {OB} \,\,\, \Leftrightarrow \,\,\overrightarrow {OA} + \overrightarrow {OB} \,\, = \overrightarrow 0 \, \Leftrightarrow \,\,O\) là trung điểm đoạn \(AB\).
Vậy tập hợp điểm \(O\) thỏa mãn \(\overrightarrow {OA} = – \overrightarrow {OB} \) chỉ có duy nhất một điểm là trung điểm của đoạn \(AB\).

