Câu 54: Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN
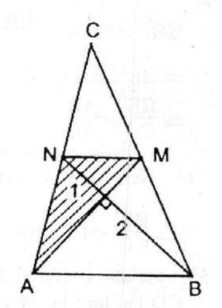
Tứ giác ABMN có hai đường chéo vuông góc.
\({S_{ABMN}} = {1 \over 2}AM.BN\)
∆ ABM và ∆ AMC có chung chiều cao kẻ từ A cạnh đáy BM = MC
\( \Rightarrow {S_{ABM}} = {S_{AMC}} = {1 \over 2}{S_{ABC}}\)
∆ MAN và ∆ MNC có chung chiều cao kẻ từ M, cạnh đáy AN = NC
\(\eqalign{ & \Rightarrow {S_{MAN}} = {S_{MNC}} = {1 \over 2}{S_{AMC}} = {1 \over 4}{S_{ABC}} \cr & {S_{ABMN}} = {S_{ABM}} + {S_{MNA}} = {1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} = {3 \over 4}{S_{ABC}} \cr & \Rightarrow {S_{ABC}} = {4 \over 3}{S_{ABMN}} = {4 \over 3}.{1 \over 2}.AM.BN = {2 \over 3}AM.BN \cr} \)
Câu 55: Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của :
a. Các tam giác DAC và DCK
b. Tam giác DAC và tứ giác ADLB
c. Các tứ giác ABKD và ABLD
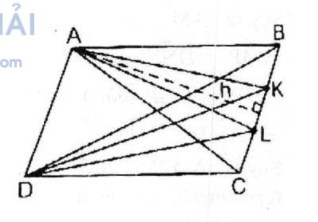
Ta có: \({S_{ACD}} = {S_{BCD}} = {S_{DAB}} = {S_{CAB}} = {1 \over 2}{S_{ABCD}}\) (1)
\(CK = {1 \over 2}CB\)
∆ DCK = ∆ DCB có chung chiều cao kẻ từ đỉnh D, cạnh đáy \(CK = {2 \over 3}CB\)
\( \Rightarrow {S_{DCK}} = {2 \over 3}{S_{DBC}}\) (2)
Từ (1) và (2) suy ra: \({S_{DCK}} = {2 \over 3}{S_{DAC}} \Rightarrow {{{S_{DCK}}} \over {{S_{DAC}}}} = {2 \over 3}\)
b. Ta có: \({S_{ADLB}} = {S_{ADB}} + {S_{DLB}}\)
Advertisements (Quảng cáo)
∆ DBC và ∆ DLC có chung chiều cao kẻ từ đỉnh D, cạnh đáy \(LB = {2 \over 3}BC\)
\( \Rightarrow {S_{DLB}} = {2 \over 3}{S_{DBC}}\)
mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)
Suy ra: \({S_{ADLB}} = {S_{DAC}} + {2 \over 3}{S_{DAC}} = {5 \over 3}{S_{DAC}} \Rightarrow {{{S_{DAC}}} \over {{S_{ADLB}}}} = {3 \over 5}\)
c. Ta có: \({S_{ABKD}} = {S_{ABD}} + {S_{DKB}}\)
∆ DKB và ∆ DCB có chung chiều cao kẻ từ D, cạnh đáy \(BL = {1 \over 3}BC\)
\( \Rightarrow {S_{DKB}} = {1 \over 3}{S_{DCB}}\)
mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)
\( \Rightarrow {S_{ABKD}} = {S_{DAC}} + {1 \over 3}{S_{DAC}} = {4 \over 3}{S_{DAC}} \Rightarrow {{{S_{ABKD}}} \over {{S_{ADLB}}}} = {{{4 \over 3}{S_{DAC}}} \over {{5 \over 3}{S_{DAC}}}} = {4 \over 5}\)
Câu 56: Cho tam giác ABC vuông ở A và có BC = 2 AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG.
a. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
b. Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE.
c. Tính diện tích tứ giác DEFG.
Advertisements (Quảng cáo)
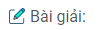
Gọi M là trung điểm của BC, ta có:
AM = MB = \({1 \over 2}\)BC = a (tính chất tam giác vuông) ⇒ AM = MB = AB = a
nên ∆ AMB đều ⇒ \(\widehat {ABC} = 60^\circ \)
Mặt khác : \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) (tính chất tam giác cân)
Suy ra: \(\widehat {ACB} = 90^\circ – \widehat {ABC} = 90^\circ – 60^\circ = 30^\circ \)
Trong tam giác vuông ABC, theo định lý Pi-ta-go ta có :
\(B{C^2} = A{B^2} + A{C^2}\)
\(\eqalign{ & \Rightarrow A{C^2} = B{C^2} – A{B^2} = 4{a^2} – {a^2} = 3{a^2} \cr & AC = a\sqrt 3 \cr} \)
\(\eqalign{ & \Rightarrow A{C^2} = B{C^2} – A{B^2} = 4{a^2} – {a^2} = 3{a^2} \cr & AC = a\sqrt 3 \cr} \) (đvdt)
b. Ta có : \(\widehat {FAB} = \widehat {ABC} = 60^\circ \)
⇒ FA // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: FA ⊥ BE
BC ⊥ CD(vì BCDE là hình vuông)
Suy ra :FA ⊥ CD
Gọi giao điểm BE và FA là H, FA và CG là K.
\( \Rightarrow BH \bot FA\)và FH = HA = \({a \over 2}\) (tính chất tam giác đều)
\(\widehat {ACG} + \widehat {ACB} + \widehat {BCD} = 60^\circ + 30^\circ + 90^\circ = 180^\circ \)
⇒ G, C, D thẳng hàng
⇒ AK ⊥ CG và GK = KC = \({1 \over 2}\) GC = \({1 \over 2}\)AC = \({{a\sqrt 3 } \over 2}\)
\({S_{FAG}} = {1 \over 2}GK.AF = {1 \over 2}.{{a\sqrt 3 } \over 2}.a = {{{a^2}\sqrt 3 } \over 4}\) (đvdt)
\({S_{FBE}} = {1 \over 2}FH.BE = {1 \over 2}.{a \over 2}.2a = {1 \over 2}{a^2}\) (đvdt)
c. \({S_{BCDE}} = B{C^2} = {\left( {2a} \right)^2} = 4{a^2}\) (đvdt)
Trong tam giác vuông BHA, theo định lý Pi-ta-go ta có:
\(\eqalign{ & A{H^2} + B{H^2} = A{B^2} \cr & \Rightarrow B{H^2} = A{B^2} – A{H^2} = {a^2} – {{{a^2}} \over 4} = {{3{a^2}} \over 4} \Rightarrow BH = {{a\sqrt 3 } \over 2} \cr} \)
\({S_{ABF}} = {1 \over 2}BH.FA = {1 \over 2}.{{a\sqrt 3 } \over 2}.a = {{{a^2}\sqrt 3 } \over 4}\) (đvdt)
Trong tam giác vuông AKC, theo định lý Pi-ta-go ta có:
\(A{C^2} = A{K^2} + K{C^2}\)
\(\eqalign{ & \Rightarrow A{K^2} = A{C^2} – K{C^2} = 3{a^2} – {{3{a^2}} \over 4} = {{9{a^2}} \over 4} \cr & AK = {{3a} \over 2} \cr} \)
\({S_{ACG}} = {1 \over 2}AK.CG = {1 \over 2}.{{3a} \over 2}.a\sqrt 3 = {{3{a^2}\sqrt 3 } \over 4}\) (đvdt)
\({S_{DEFG}} = {S_{BCDE}} + {S_{FBE}} + {S_{FAB}} + {S_{FAG}} + {S_{ACG}}\)
\( = 4{a^2} + {{{a^2}} \over 2} + {{{a^2}\sqrt 3 } \over 4} + {{{a^2}\sqrt 3 } \over 4} + {{3{a^2}\sqrt 3 } \over 4} = {{{a^2}} \over 4}\left( {18 + 5\sqrt 3 } \right)\) (đvdt)

