Câu 22: Cho hình bình hành ABCD (h. 184). Đường phân giác của các góc A và C cắt đường chéo BD tai E, F.
a. Chứng minh rằng hai hình ABCFE và ADCFE có cùng diện tích.
b. Các hình đó có phải đa giác lồi ko ? Vì sao ?


∆ ABE = ∆ CDF (g.c.g)
\( \Rightarrow {S_{ABE}} = {S_{CDF}}\) (1)
Ta có: ∆ AED = ∆ CFB (g.c.g)
\( \Rightarrow {S_{AED}} = {S_{CFB}}\) (2)
Từ (1) và (2) suy ra:
\({S_{ABE}} + {S_{CFB}} = {S_{CDF}} + {S_{AED}}\)
Hay \({S_{ABCFE}} = {S_{ADCFE}}\)
Advertisements (Quảng cáo)
b. Hình ABCFE không phải đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Hình ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Câu 23: Trên hình 185, các tứ giác ABCD và EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC.
a. Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích.
b. ABCFE có phải là đa giác lồi không ? Vì sao ?

Advertisements (Quảng cáo)

a. Ta có: ∆ ABC = ∆ CDA (c.c.c)
\( \Rightarrow {S_{ABC}} = {S_{CDA}}\) (1)
∆ EFC = ∆ CHE (c.c.c)
\( \Rightarrow {S_{EFC}} = {S_{CHE}}\) (2)
Từ (1) và (2) suy ra:
\({S_{ABC}} – {S_{EFC}} = {S_{CDA}} – {S_{CHE}}\)
Hay \({S_{ABCFE}} = {S_{AEHD}}\)
b. Hình ABCFE không phải tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.
Câu 24: Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền(không sử dụng định lý Py-ta-go)

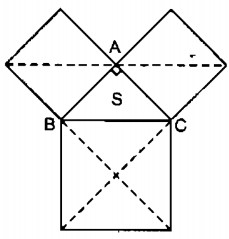
Gọi S là diện tích của tam giác ABC
Hình vuông có cạnh AB chia thành hai tam giác vuông cân bằng ∆ ABC nên diện tích hình vuông cạnh AB bằng 2S
Hình vuông có cạnh AC chia thành hai tam giác vuông cân bằng ∆ ABC nên có diện tích bằng 2S
Hình vuông BC chia thành 4 hình tam giác vuông cân bằng ∆ ABC nên có diện tích bằng 4S
Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên hai cạnh huyền bằng tổng diên tích hai hình vuông dựng trên hai cạnh góc vuông.

