Câu 25: Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không ? Vì sao ?
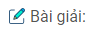
Gọi O là giao điểm hai đường chéo hình chữ nhật ABCD
⇒ OA = OB = OC = OD (tính chất hình chữ nhật)
∆ OAB = ∆ OCD (c.g.c) \( \Rightarrow {S_{OAB}} = {S_{OCD}}\) (1)
∆ OAD = ∆ OBC (c.g.c) \( \Rightarrow {S_{OAD}} = {S_{OBC}}\) (2)
Kẻ AH ⊥ BD
\(\eqalign{ & {S_{OAD}} = {1 \over 2}AH.OD \cr & {S_{OAB}} = {1 \over 2}AH.OB \cr} \)
Advertisements (Quảng cáo)
Suy ra: \({S_{OAD}} = {S_{OAB}}\) (3)
Từ (1), (2) và (3) suy ra:
\({S_{OAB}} = {S_{OBC}} = {S_{OCD}} = {S_{ODA}}\)
Câu 26: Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi.
Advertisements (Quảng cáo)
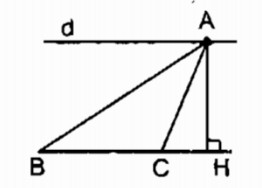
∆ ABC có đáy BC không đổi, chiều cao AH là khoảng cách giữa hai đường thẳng song song không đổi. Vậy điểm A thay đổi trên đường thẳng d // BC thì \({S_{ABC}}\) không đổi.
Câu 27: Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC.
a. Điền vào ô trống trong bảng sau:
|
Độ dài AH (cm) |
1 |
2 |
3 |
4 |
5 |
10 |
15 |
20 |
|
\({S_{ABC}}\)\(\left( {c{m^2}} \right)\) |
|
|
|
|
|
|
|
|
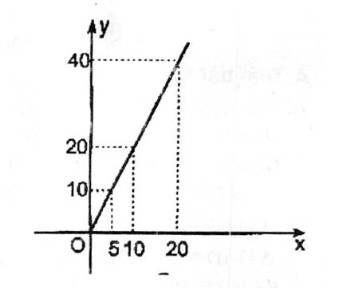
b. Vẽ đồ thị biểu diễn số đo \({S_{ABC}}\) theo độ dài AH
c. Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không ?
a. Điền vào chỗ trống
|
Độ dài AH (cm) |
1 |
2 |
3 |
4 |
5 |
10 |
15 |
20 |
|
\({S_{ABC}}\) \(\left( {c{m^2}} \right)\) |
2 |
4 |
6 |
8 |
10 |
20 |
30 |
40 |
b. \({S_{ABC}}\)là hàm số của chiều cao AH.
Gọi y là diện tích của ∆ ABC \(\left( {c{m^2}} \right)\) và độ dài x là độ dài AH (cm) thì y = 2x
Ta có đồ thị như hình bên.
c. Diện tích của tam giác tỉ lệ thuận với chiều cao.

