Câu 19: Tính diện tích các hình trên hình 182 (mỗi ô vuông là một đơn vị diện tích ).
Hãy giải thích vì sao được tính như vậy.
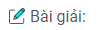
Hình A cắt rời hai thành tam giác ghép lại được một hình chữ nhật có một cạnh 3 ô vuông và một cạnh 2 ô vuông nên có diện tích 6 ô vuông (6 đơn vị diện tích)
Hình B là một hình thang cân, cắt theo đường cao kẻ từ một đỉnh của đáy nhỏ ghép lại ta được một hình chữ nhật có cạnh 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 6 ô vuông (6 đơn vị diện tích)
Hình C là hình thang vuông, cắt phần nhọn ghép lên ta được một hình chữ nhật có một cạnh là 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 6 ô vuông (6 đơn vị diện tích)
Hình D ta lấy diện tích hình vuông có cạnh 5 ô vuông trừ đi phần khuyết của 4 góc mỗi góc là một nửa ô vuông ta có diện tích là 5 x 5 – 4 . = 25 – 2 = 23 ô vuông (23 đơn vị diện tích).
Advertisements (Quảng cáo)
Câu 20: Trên giấy kẻ ô vuông, hãy vẽ:
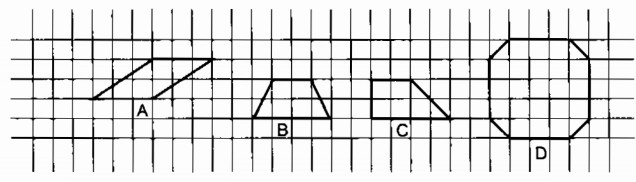
a. Hai hình chữ nhật có cùng chu vi nhưng khác diện tích.
b. Hai hình chữ nhật có kích thước khác nhau nhưng cùng diện tích.
Hình vẽ sau đây
Advertisements (Quảng cáo)
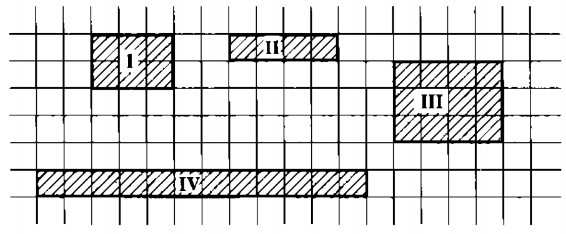
Câu 21: Cho hình bình hành ABCD (h. 183). Từ A và C kẻ AH và CK vuông góc với đường chéo BD. Chứng minh rằng hai đa giác ABCH và ADCK có cùng diện tích.
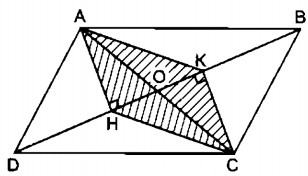
Ta có: ∆ ABC = ∆ ADC (c.c.c)
\( \Rightarrow {S_{ABC}} = {S_{ADC}}\) (1)
∆ AHC = ∆ AKC (c.c.c)
\( \Rightarrow {S_{AHC}} = {S_{AKC}}\) (2)
Từ (1) và (2) suy ra:
\({S_{ABC}} + {S_{AHC}} = {S_{ADC}} + {S_{AKC}}\)
hay \({S_{ABCH}} = {S_{ADCK}}\)

