Câu 32: Tính x, biết đa giác ở hình 188 có diện tích là 3375 m2.
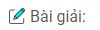
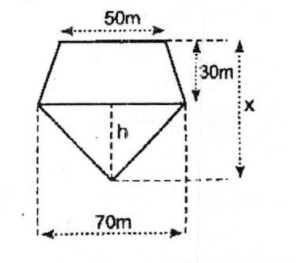
Hình đa giác đã cho gồm một hình thang và một hình tam giác.
Diện tích phần hình thang là S1, tam giác là S2
\({S_1} = {{50 + 70} \over 2}.30 = 1800\) (\({m^2}\))
\({S_2} = S – {S_1} = 3375 – 1800 = 1575\) (\({m^2}\))
Chiều cao h của tam giác là:
\(H = {{2{S_2}} \over {70}} = {{2.1575} \over {70}} = 45\) (m)
Độ dài x = 45 + 30 = 75 (m)
Câu 33: Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được bao nhiêu hình ABEF như vậy ?
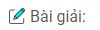
Advertisements (Quảng cáo)
Trên cạnh CD ta lấy 1 điểm E bất kỳ (E khác C và D). Nối BE. Từ A kẻ đường thẳng song song với BE cắt đường thẳng CD tại F. Ta có hình bình hành ABEF có cạnh AB và có diện tích bằng diện tích hình chữ nhật.
Thật vậy : SABCD = AB . AD
SABEF = AB . AD ⇒ SABCD = SABEF
Ta vẽ được vô số hình như vậy
Câu 34: Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có các cạnh AB = 5cm, BE = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được mấy hình ABEF như vậy ?
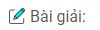
Advertisements (Quảng cáo)
Vẽ cung tròn tâm B bán kính 5cm cắt Đường thẳng CD tại hai điểm E và E’ (vì ta có BA > BC)
Nối BE, từ A kẻ đường thẳng song song với BE cắt đường thẳng CD tại F
Nối BE’, từ A kẻ đường thẳng song song với BE’ cắt đường thẳng CD tại F’
Ta có hình bình hành ABEF và hình bình hành ABE’F’ có cạnh AB = 5cm, BE = 5cm, BE’ = 5cm có diện tích bằng diện tích hình chữ nhật ABCD. Vẽ được hai hình.
Câu 35: Tính diện tích của một hình thang vuông, biết hai đáy có độ dài là 2cm và 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng 450.
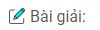
Xét hình thang vuông ABCD có: \(\widehat A = \widehat D = {90^0};\widehat C = {45^0}\)
Kẻ BE ⊥ CD
Trong tam giác vuông BEC có \(\widehat {BEC} = {90^0}\)
\(\widehat C = 45^\circ \Rightarrow \)∆ BEC vuông cân tại E
⇒ BE = EC
Hình thang ABED có hai cạnh bên AD // BE (vì cùng vuông góc với DC)
⇒ DE = AB = 2cm
EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm
\({S_{ABCD}} = {1 \over 2}.BE\left( {AB + CD} \right) = {1 \over 2}.2.\left( {2 + 4} \right) = 6(c{m^2})\)

