Câu 5: Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.
Áp dụng công thức tính ố đo mỗi góc của đa giác đều có n cạnh bằng \({{\left( {n – 2} \right){{.180}^0}} \over n}\)
– Đa giác đều 8 cạnh ⇒ n = 8, ố đo mỗi góc là : \({{\left( {8 – 2} \right){{.180}^0}} \over 8} = {135^0}\)
– Đa giác đều 10 cạnh ⇒ n = 10, ố đo mỗi góc là : \({{\left( {10 – 2} \right){{.180}^0}} \over {10}} = {144^0}\)
– Đa giác đều 12 cạnh ⇒ n = 12, ố đo mỗi góc là : \({{\left( {12 – 2} \right){{.180}^0}} \over {12}} = {150^0}\)
Câu 6: a. Vẽ hình và tính ố đường chéo của ngũ giác, lục giác
b. Chứng minh rằng hình n – giác có tất cả \(({{n\left( {n – 3} \right)} \over 2}\) đường chéo.
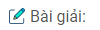
Advertisements (Quảng cáo)
a. Từ mỗi đỉnh của ngũ giác vẽ được hai đường chéo. Ngũ giác có 5 đỉnh ta kẻ được 5.2 = 10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.
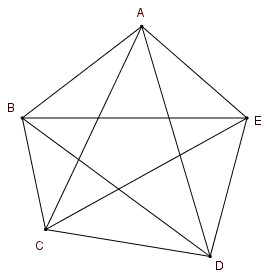
Từ mối đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả là 9 đường chéo.
b. Từ mỗi đỉnh của n – giác nối với các đỉnh còn lại ta được n – 1 đoạn thẳng , trong đó có hai đoạn thẳng là cạnh của hình n – giác (hai đoạn thẳng nối với hai đỉnh kề nhau). Vậy qua mỗi đỉnh của n – giác vẽ được n – 3 đường chéo. Hình n – giác có n đỉnh kẻ được n(n – 3 ) đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy hình n – giác có tất cả \({{n\left( {n – 3} \right)} \over 2}\) đường chéo.
Câu 7: Tìm số đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh.
Advertisements (Quảng cáo)
Áp dụng công thức tính ở bài 6.
Đa giác có 8 cạnh, số đường chéo là : \({{8\left( {8 – 3} \right)} \over 2} = 20\) đường chéo
Đa giác có 10 cạnh, số đường chéo là : \({{10\left( {10 – 3} \right)} \over 2} = 35\) đường chéo
Đa giác có 12 cạnh, số đường chéo là : \({{12\left( {12 – 3} \right)} \over 2} = 54\)đường chéo.
Câu 8: Chứng minh rằng tổng các góc ngoài của một đa giác (lồi ) có ố đo là 360°.
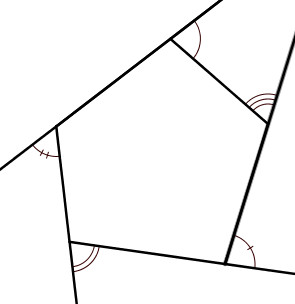
Tổng ố đo của góc trong và góc ngoài ở mỗi đỉnh của hình n – giác bằng 180°
Hình n – giác có n đỉnh nên tổng ố đo các góc trong và góc ngoài của đa giác bằng n . 180°
Mặt khác ta biết tổng các góc trong của hình n – giác bằng (n – 2 ). 180°
Vậy tổng ố đo các góc ngoài của hình n – giác là:
n . 180° – (n – 2) . 180°= n . 180° – n .180° +2. 180°= 360°

