Câu 48: Cho tam giác ABC (\(\widehat A = 90^\circ \)) có đường cao AH (h.34)
Chứng minh rằng \(A{H^2} = BH.CH\)
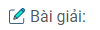
(hình 34 trang 95 sbt)
Xét hai tam giác vuông HBA và HAC, ta có:
\(\widehat {HBA} = \widehat {AHC} = 90^\circ \)
\(\widehat B = \widehat {HAC}\) (hai góc cùng phụ góc C)
Suy ra: ∆ HBA đồng dạng ∆ HAC (g.g)
Suy ra: \({{HA} \over {HB}} = {{HC} \over {HA}}\)
Vậy \(A{H^2} = HB.HC\)
Câu 49: Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16cm. Tính độ dài các cạnh của tam giác vuông đó (h.35)
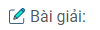
Advertisements (Quảng cáo)
(hình 35 trang 96 sbt)
Xét hai tam giác vuông DAC và DBA, ta có:
\(\widehat {ADC} = \widehat {BDA} = 90^\circ \)
\(\widehat C = \widehat {DAB}\) (hai góc cùng phụ góc B)
Suy ra: ∆ DAC đồng dạng ∆ DBA (g.g)
Suy ra: \({{DB} \over {DA}} = {{DA} \over {DC}} = {{AC} \over {BC}}\)
\( \Rightarrow D{A^2} = DB.DC\)
Advertisements (Quảng cáo)
hay \(DA = \sqrt {DB.DC} = \sqrt {9.16} = 12\) (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
\(\eqalign{ & A{B^2} = D{A^2} + D{B^2} = {9^2} + {12^2} = 225 \cr & \Rightarrow AB = 15(cm) \cr} \)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD, ta có:
\(\eqalign{ & A{C^2} = D{A^2} + D{C^2} = {12^2} + {16^2} = 400 \cr & AC = 20(cm) \cr} \)
Vậy \(BC = BD + DC = 9 + 16 = 25\) (cm)
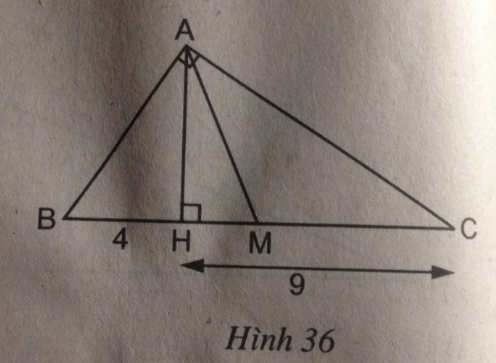
Câu 50: Tam giác vuông ABC (\(\widehat A = 90^\circ \)) có đường cao AH và trung tuyến AM (h.36). Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm.
(hình 36 trang 96 sbt)
Xét hai tam giác vuông HBA và HAC, ta có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat C = \widehat {HAC}\) (hai góc cùng phụ góc C)
Suy ra: ∆ HBA đồng dạng ∆ HAC (g.g)
Suy ra: ${{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\) (cm)
Suy ra: AH = 6(cm)
Lại có: \(BM = {1 \over 2}BC = {1 \over 2}.\left( {9 + 4} \right) = {1 \over 2}.13 = 6,5\) (cm)
Mà \(HM = BM – BH = 6,5 – 4 = 2,5\) (cm)
Vậy \({S_{AHM}} = {1 \over 2}AH.HM = {1 \over 2}.6.2,5 = 7,5(c{m^2})\)

