Câu 36: Một cái chặn giấy bằng thủy tinh hình lăng trụ đứng có các kích thước cho ở hình 126. Diện tích toàn phần của nó là:
A. 840cm2
B. 620cm2
C. 670cm2
D. 580cm2
E. 600cm2
Hãy chọn kết quả đúng.

Diện tích xung quanh hình lăng trụ:
\({S_{xq}} = 10.10 + 10.24 + 10.26 = 600(c{m^2})\)
Diện tích mặt đáy hình lăng trụ:
Sđáy \( = {1 \over 2}.10.24 = 120(c{m^2})\)
Diện tích toàn phần hình lăng trụ:
STP = Sxq + 2.Sđáy \( = 600 + 2.120 = 840(c{m^2})\)
Vậy chọn đáp án A.
Câu 37: Đáy của lăng trụ đứng là một hình thang cân có các cạnh b = 11mm, a = 15mm và chiều cao hT = 7mm (h.127)
Advertisements (Quảng cáo)
Chiều cao của hình lăng trụ là h = 14mm. Tính diện tích xung quanh của lăng trụ.


Giả sử hình lăng trụ có CD = 11mm;
AB = 15mm; DH = 7mm.
Ta có: \(AH = {{AB – CD} \over 2} = {{15 – 11} \over 2} = 2(mm)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHD, ta có:
\(\eqalign{ & A{D^2} = A{H^2} + H{D^2} = {2^2} + {7^2} \cr & = 4 + 49 = 53 \cr} \)
Suy ra: \(AD = \sqrt {53} (mm)\)
Vì ABCD là hình thang cân nên BC = AD
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{ & {S_{xq}} = \left( {AB + BC + DC + AD} \right).BB’ \cr & = \left( {AB + DC + 2AD} \right).BB’ \cr & = \left( {15 + 11 + 2\sqrt {53} } \right).14 \cr & = \left( {364 + 28\sqrt {53} } \right)(m{m^2}) \cr} \)
Câu 38: Cho hình hộp chữ nhật DE1BG1.HF1EG có dạng như hình 128.
Người ta lấy các trung điểm A, C, I, F của các cạnh tương ứng thuộc đáy trên và đáy dưới. Hình DABC.HFEI nhận được là một lăng trụ đứng, một hình hộp chữ nhật, hay một hình lập phương ?
(xem hình 128)


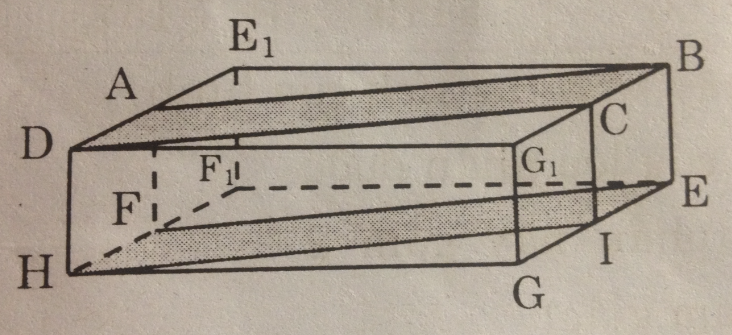
Hình DABC.HFEI nhận được là một lăng trụ đứng có đáy DABC là một hình bình hành, các mặt bên là hình chữ nhật.
Câu 39: Một lăng trụ đứng lục giác đều có độ dài cạnh đáy là 6cm, chiều cao của lăng trụ là 10 cm. Diện tích toàn phần của lăng trụ đó là (đơn vị cm2):
A. \(180 + 54\sqrt {3;} \)
B. \(180 + 108\sqrt {3;} \)
C. \(360 + 54\sqrt {3;} \)
D. \(360 + 108\sqrt {3.} \)
Hãy chọn kết quả đúng.

Nối các đường chéo AD, BE, CF của mặt đáy.
Các đường chéo chia lục giác ra thành 6 tam giác đều bằng nhau có cạnh là 6(cm).
Diện tích mặt đáy bằng diện tích một tam giác đều cạnh 6cm nhân với 6.
Diện tích một tam giác đều cạnh 6cm là \(9\sqrt 3 (c{m^2})\)
Diện tích một mặt đáy là \(54\sqrt 3 (c{m^2})\)
Diện tích xung quanh của hình trụ là: \(6.10.6 = 360(c{m^2})\)
Ta có: STP = Sxq + 2.Sđáy = \(360 + 2.54.\sqrt 3 = 360 + 108\sqrt 3 (c{m^2})\)
Vậy chọn đáp án D.

