Câu 29: Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không ?
a. 4cm, 5cm, 6cm và 8mm, 10mm, 12mm;
b. 3cm, 4cm, 6cm và 9cm, 15cm, 18cm;
c. 1dm, 2dm, 2dm và 1dm, 1dm, 0,5dm.
a. Ta có: \({4 \over 8} = {5 \over {10}} = {6 \over {12}}\). Vậy hai tam giác đó đồng dạng
b. Ta có: \({3 \over 9} = {6 \over {12}} \ne {4 \over {15}}\). Vậy hai tam giác đó không đồng dạng
c. Ta có: \({1 \over 2} = {1 \over 2} = {{0,5} \over 1}\). Vậy hai tam giác đó đồng dạng.
Câu 30: Tam giác vuông ABC (\(\widehat A = 90^\circ \)) có AB = 6cm, AC = 8cm và tam giác vuông A’B’C’ (\(\widehat {A’} = 90^\circ \)) có A’B’ = 9cm, B’C’ = 15cm.
Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không ? Vì sao ?
Trong tam giác vuông A’B’C’ có \(\widehat {A’} = 90^\circ \)
Advertisements (Quảng cáo)
Áp dụng định lí Pi-ta-go, ta có: \(A’B{‘^2} + A’C{‘^2} = B’C{‘^2}\)
Suy ra: \(A’C{‘^2} = B’C{‘^2} – A’B{‘^2} = {15^2} – {9^2} = 144\)
Suy ra: A’C’ =12 (cm)
Trong tam giác vuông ABC có \(\widehat A = 90^\circ \)
Áp dụng định lí Pi-ta-go, ta có: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\)
Suy ra: BC = 10 (cm)
Ta có: \({{A’B’} \over {AB}} = {9 \over 6} = {3 \over 2};{{A’C’} \over {AC}} = {{12} \over 8} = {3 \over 2};{{B’C’} \over {BC}} = {{15} \over {10}} = {3 \over 2}\)
Advertisements (Quảng cáo)
Suy ra: \({{A’B’} \over {AB}} = {{A’C’} \over {AC}} = {{B’C’} \over {BC}} = {3 \over 2}\)
Vậy ∆ A’B’C’ đồng dạng ∆ ABC (c.c.c).
Câu 31: Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P, Q, R thứ tự là trung điểm của các đoạn thẳng OA, OB, OC.
Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
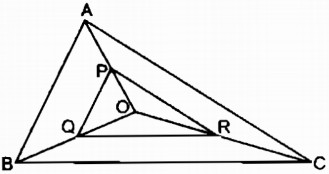
Trong ∆ OAB, ta có PQ là đường trung bình nên:
\(PQ = {1 \over 2}AB\) (tính chất đường trung bình của tam giác )
Suy ra: \({{PQ} \over {AB}} = {1 \over 2}\) (1)
Trong ∆ OAC, ta có PR là đường trung bình nên:
\(PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{PR} \over {AC}} = {1 \over 2}\) (2)
Trong ∆ OBC, ta có QR là đường trung bình nên:
\(QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{QR} \over {BC}} = {1 \over 2}\) (3)
Từ (1), (2) và (3) suy ra: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}}\)
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c).

