Câu 51: Cho tam giác ABC.
a. Tìm trên cạnh AB điểm M sao cho \({{AM} \over {MB}} = {2 \over 3}\); tìm trên cạnh AC điểm N sao cho \({{AN} \over {NC}} = {2 \over 3}\)
b. Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không ? Vì sao ?
c. Cho biết chu vi và diện tích tam giác ABC thứ tự là P và S. Tính chu vi và diện tích tam giác AMN.
a. Cách vẽ:
– Kẻ tia Ax bất kì khác tia AB, AC.
– Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đvd), EF = 3 (đvd)
– Kẻ đường thẳng FB.
– Từ E kẻ đường thẳng song song với FB cắt AB tại M
– Kẻ đường thẳng FC
– Từ E kẻ đường thẳng song song với FC cắt AC tại N
Ta có M, N là hai điểm cần vẽ.
Chứng minh:
Trong tam giác AFB, ta có: EM // FB
Theo Định lí Ta-lét, ta có:
\({{AM} \over {MB}} = {{AE} \over {EF}} = {2 \over 3}\)
Trong tam giác AFC, ta có: EN // FC
Theo Định lí Ta-lét, ta có:
\({{AN} \over {NB}} = {{AE} \over {EF}} = {2 \over 3}\)
Vậy M, N là hai điểm cần tìm.
b. Trong tam giác ABC, ta có: \({{AM} \over {MB}} = {{AN} \over {NC}} = {2 \over 3}\)
Suy ra: MN // BC (theo định lí đảo của định lí Ta-lét)
c. Gọi p’ và S’ là chu vi và diện tích của ∆ AMN
Trong tam giác ABC, ta có: MN // BC
Suy ra: ∆ AMN đồng dạng ∆ ABC
Theo tính chất hai tam giác đồng dạng ta có:
\(\eqalign{ & {{p’} \over p} = {2 \over 3} = k \Rightarrow p’ = {2 \over 3}p \cr & {{S’} \over S} = {\left( {{2 \over 3}} \right)^2} = {4 \over 9} = {k^2} \Rightarrow S’ = {4 \over 9}S \cr} \)
Câu 52: Tứ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O, \(\widehat {BAO} = \widehat {BDC}\) (h.37)
Chứng minh:
a. ∆ ABO đồng dạng ∆ DCO
Advertisements (Quảng cáo)
b. ∆ BCO đồng dạng ∆ ADO
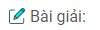
(hình 37 trang 97 sbt)
a. Xét ∆ABO và ∆ DCO, ta có:
\(\widehat {BAO} = \widehat {BDC}\) (gt)
hay \(\widehat {BAO} = \widehat {ODC}\)
\(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)
Vậy ∆ ABO đồng dạng ∆ DCO (g.g)
b. Vì ∆ ABO đồng dạng ∆ DCO nên:
\({\widehat B_1} = {\widehat C_1}\) (1)
Mà \({\widehat C_1} + {\widehat C_2} = \widehat {BCD} = 90^\circ \) (2)
Trong tam giác ABD, ta có: \(\widehat A = 90^\circ \)
Suy ra: \({\widehat B_1} + {\widehat D_2} = 90^\circ \) (3)
Từ (1) , (2) và (3) suy ra : \({\widehat C_2} = {\widehat D_2}\)
Xét ∆ BCO và ∆ ADO, ta có:
\({\widehat C_2} = {\widehat D_2}\) (chứng minh trên )
\(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh)
Vậy ∆ BOC đồng dạng ∆ ADO (g.g)
Câu 53: Cho hình chữ nhật ABCD có AB = a = 12 cm, BC = b = 9cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD (h.38)
Advertisements (Quảng cáo)
a. Chứng minh ∆ AHB đồng dạng ∆ BCD;
b. Tính độ dài đoạn thẳng AH;
c. Tính diện tích tam giác AHB.
(hình 38 trang 97 sbt)
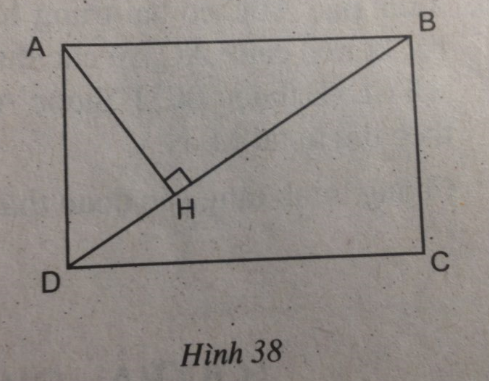
Xét ∆ AHB và ∆ BCD, ta có:
\(\widehat {AHB} = \widehat {BCD} = 90^\circ \)
AB // CD (gt)
\(\widehat {ABH} = \widehat {BDC}\) (so le trong)
Vậy ∆ AHB đồng dạng ∆ BCD (g.g)
b. Vì ∆ AHB đồng dạng ∆ BCD nên:
\({{AH} \over {BC}} = {{AB} \over {BD}}\)
Suy ra: \(AH = {{AB.BC} \over {BD}}\)
Áp dụng định lí Pi-ta-go vào tam giác vuông BCD, ta có:
\(\eqalign{ & B{D^2} = B{C^2} + C{D^2} = B{C^2} + A{B^2} \cr & = {12^2} + {9^2} = 225 \cr} \)
Suy ra: BD = 15 (cm)
Vậy \(AH = {{12.9} \over {15}} = 7,2\) (cm).
c. Vì ∆ AHB đồng dạng ∆ BCD nên k = \({{AH} \over {BC}} = {{7,2} \over 9} = 0,8\)
Ta có: \({{{S_{AHB}}} \over {{S_{BCD}}}} = {k^2} = {\left( {0,8} \right)^2} = 0,64 \Rightarrow {S_{AHB}} = 0,64{S_{BCD}}\)
\({S_{BCD}} = {1 \over 2}BC.CD = {1 \over 2}.12.9 = 54(c{m^2})\)
Vậy \({S_{AHB}} = 0,64.{S_{BCD}} = 0,64.54 = 34,56(c{m^2})\)
Câu 54: Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, \(\widehat {ABD} = \widehat {ACD}\).Gọi E là giao điểm của hai đường thẳng AD và BC (h.39)
Chứng minh rằng :
a. ∆ AOB đồng dạng ∆ DOC
b. ∆ AOD đồng dạng ∆ BOC
c. EA.ED = EB.EC
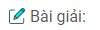
(hình 39 trang 97 sbt)
a. Xét ∆ AOB và ∆ DOC, ta có:
\(\widehat {ABD} = \widehat {ACD}\)(gt)
Hay \(\widehat {ABO} = \widehat {OCD}\)
\(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)
Vậy ∆ AOB đồng dạng ∆ DOC (g.g)
b. Vì ∆ AOB đồng dạng ∆ DOC nên:
\({{AO} \over {DO}} = {{OB} \over {OC}} \Rightarrow {{AO} \over {OB}} = {{DO} \over {OC}}\)
Xét ∆ AOD và ∆ BOC, ta có:
\({{AO} \over {OB}} = {{DO} \over {OC}}\)
\(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)
Vậy ∆ AOD đồng dạng ∆ BOC (c.g.c)
c. Vì ∆ AOD đồng dạng ∆ BOC nên:
\(\widehat {ADO} = \widehat {BCO}\)
hay \(\widehat {EDB} = \widehat {ECA}\)
Xét ∆ EDB và ∆ ECA, ta có:
\(\widehat E\) chung
\(\widehat {EDB} = \widehat {ECA}\) (chứng minh trên )
Vậy ∆ EDB đồng dạng ∆ ECA (g.g)
Suy ra: \({{ED} \over {EC}} = {{EB} \over {EA}} \Rightarrow ED.EA = EC.EB\)

