Câu 39: Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh hai tam giác ADE và CBF đồng dạng với nhau.
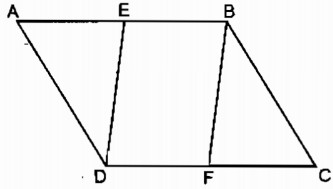
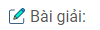
Vì ABCD là hình bình hành nên:
AB = CD (1)
Theo giả thiết:
AE = EB = \({1 \over 2}AB\) (2)
\(DF = FC = {1 \over 2}CD\) (3)
Từ (1), (2) và (3) suy ra:
EB = DF và BE // DF
Suy ra tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
Suy ra: DE // BF
Ta có: \(\widehat {AED} = \widehat {ABF}\) (đồng vị)
\(\widehat {ABF} = \widehat {BFC}\) (so le trong)
Suy ra: \(\widehat {AED} = \widehat {BFC}\)
Xét ∆ AED và ∆ CFB, ta có:
\(\widehat {AED} = \widehat {BFC}\) (chứng minh trên )
\(\widehat A = \widehat C\) (tính chất hình bình hành)
Vậy: ∆ AED đồng dạng ∆ CFB (g.g)
Câu 40: Tam giác vuông ABC có $\widehat A = 90^\circ $ và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27).
Advertisements (Quảng cáo)
a. Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b. Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.
(hình 27 trang 93 sbt)
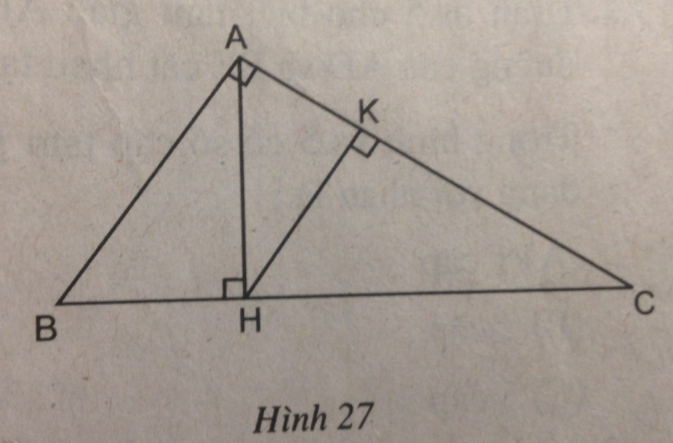
a. Trong hình bên có 5 tam giác đồng dạng với nhau theo từng đôi một, đó là: ∆ABC; ∆ HAB; ∆ HAC; ∆ KAH; ∆ KHC.
b. Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:
– ∆ ABC đồng dạng ∆ HAB. Ta có: \({{AB} \over {HA}} = {{AC} \over {HB}} = {{BC} \over {AB}}\)
– ∆ ABC đồng dạng ∆ HAC . Ta có: \({{AB} \over {HA}} = {{AC} \over {HC}} = {{BC} \over {AC}}\)
– ∆ ABC đồng dạng ∆ KHC. Ta có: \({{AB} \over {KH}} = {{AC} \over {KC}} = {{BC} \over {HC}}\)
– ∆ ABC đồng dạng ∆ KAH. Ta có: \({{AB} \over {KA}} = {{AC} \over {KH}} = {{BC} \over {AH}}\)
– ∆ HAB đồng dạng ∆ HAC. Ta có: \({{HB} \over {HA}} = {{HA} \over {HC}} = {{BA} \over {AC}}\)
– ∆ HAB đồng dạng ∆ KHC. Ta có: \({{HB} \over {KH}} = {{HA} \over {KC}} = {{BA} \over {HC}}\)
– ∆ HAB đồng dạng ∆ KAH. Ta có: \({{HB} \over {KA}} = {{HA} \over {KH}} = {{BA} \over {AH}}\)
Advertisements (Quảng cáo)
– ∆ HAC đồng dạng ∆ KHC. Ta có: \({{HA} \over {KH}} = {{HC} \over {KC}} = {{AC} \over {HC}}\)
– ∆ HAC đồng dạng ∆ KAH. Ta có: \({{HA} \over {KA}} = {{HC} \over {KH}} = {{AC} \over {AH}}\)
– ∆ KHC đồng dạng ∆ KAH. Ta có: \({{KH} \over {KA}} = {{KC} \over {KH}} = {{HC} \over {AH}}\)
Câu 41: Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và \(\widehat {DAB} = \widehat {DBC}\) (h.28).
a. Chứng minh ∆ ADB đồng dạng ∆ BCD
b. Tính độ dài các cạnh BC, CD
c. Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.
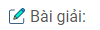
(hình 28 trang 94 sbt)
Xét ∆ ABD và ∆ BDC, ta có:
\(\widehat {DAB} = \widehat {DBC}\) (gt)
\(\widehat {ABD} = \widehat {BDC}\) (so le trong)
Suy ra: ∆ ABD đồng dạng ∆ BDC (g.g)
b. Vì ∆ ABD đồng dạng ∆ BDC nên : \({{AB} \over {BD}} = {{AD} \over {BC}} = {{BD} \over {DC}}\)
Với AB = 2,5; AD = 3,5; BD = 5, ta có:
\(\eqalign{ & {{2,5} \over 5} = {{3,5} \over {BC}} = {5 \over {DC}} \cr & \Rightarrow BC = {{5.3,5} \over {2,5}} = 7(cm) \cr} \)
Vậy DC = \({{5,5} \over {2,5}} = 10\) (cm)
Câu 42: Cho tam giác vuông ABC (\(\widehat A = 90^\circ \)). Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F (h.29).
Chứng minh: \({{FD} \over {FA}} = {{EA} \over {EC}}\).
(hình 29 trang 94 sbt)
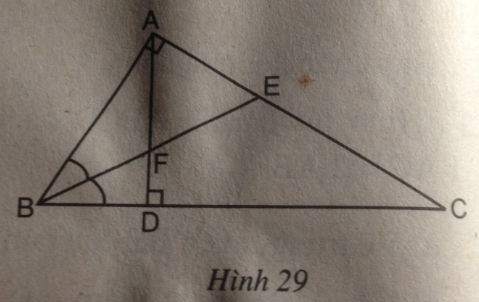
Trong tam giác ABC, ta có: BE là tia phân giác của góc ABC
Suy ra: \({{EA} \over {EC}} = {{AB} \over {BC}}\) (tính chất đường phân giác ) (1)
Trong tam giác ADB, ta có: BF là tia phân giác của góc ABD
Suy ra: \({{FD} \over {FA}} = {{BD} \over {BA}}\) (tính chất đường phân giác ) (2)
Xét ∆ ABC và ∆ DAB, ta có:
\(\widehat {BAC} = \widehat {BDA} = 90^\circ \)
\(\widehat B\) chung
Suy ra: ∆ ABC đồng dạng ∆ DBA (g.g)
Suy ra: \({{BD} \over {BA}} = {{AB} \over {BC}}\) (3)
Từ (1), (2) và (3) suy ra: \({{FD} \over {FA}} = {{EA} \over {EC}}\)

