Câu 55: Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH
(hình trang 121 sgbt)
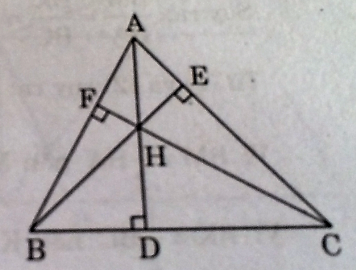
Xét ∆ AFH và ∆ CDH, ta có:
\(\widehat {AFH} = \widehat {CDH} = 90^\circ \)
\(\widehat {AHF} = \widehat {CHD}\) (đối đỉnh)
Suy ra: ∆ AFH đồng dạng ∆ CDH (g.g)
Suy ra: \({{AH} \over {CH}} = {{FH} \over {DH}}\)
Suy ra: AH.DH = CH.FH (1)
Xét ∆ AEH và ∆ BDH, ta có:
\(\widehat {AEH} = \widehat {BDH} = 90^\circ \)
\(\widehat {AHE} = \widehat {BHD}\) (đối đỉnh)
Suy ra: ∆ AEH đồng dạng ∆ BDH (g.g)
Suy ra: \({{AH} \over {BH}} = {{EH} \over {DH}}\)
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.
Câu 56: Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại điểm P. Biết rằng AP = 2 PK và CP = 2PM.
Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC.
(hình trang 121 sgbt)
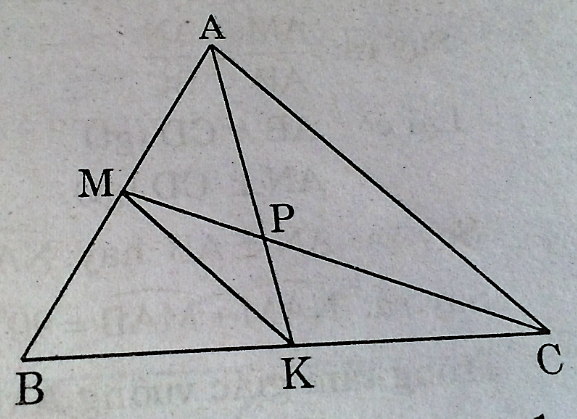
Xét ∆ PAC và ∆ PKM, ta có:
\({{PK} \over {PA}} = {1 \over 2};{{PM} \over {PC}} = {1 \over 2}\)
Suy ra: \({{PK} \over {PA}} = {{PM} \over {PC}} = {1 \over 2}\)
Advertisements (Quảng cáo)
Lại có: \(\widehat {APC} = \widehat {KPM}\) (đối đỉnh)
Suy ra: ∆ PKM đồng dạng ∆ PAC (c.g.c) với tỉ số đồng dạng k = \({1 \over 2}\)
Suy ra: \({{KM} \over {AC}} = {1 \over 2}\) (1)
Vì ∆ PKM đồng dạng ∆ PAC nên:
\(\widehat {PKM} = \widehat {PAC}\)
Suy ra: KM // AC (vì có cặp góc ở vị trí so le trong bằng nhau)
Trong tam giác ABC, ta có: KM // AC
Suy ra: ∆ BMK đồng dạng ∆ BAC (g.g)
Suy ra: \({{BM} \over {BA}} = {{BK} \over {BC}} = {{MK} \over {AC}}\) (2)
Từ (1) và (2) suy ra : \({{BM} \over {BA}} = {{BK} \over {BC}} = {1 \over 2}\)
Vì BM = \({1 \over 2}\) BA nên M lừ trung điểm AB
Vì BK = \({1 \over 2}\) BC nên K là trung điểm của BC.
Vậy BK và CM là đường trung tuyến của tam giác ABC.
Câu 57: Cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc với CD(M thuộc BC và N thuộc CD). Chứng minh rằng tam giác MAN đồng dạng với tam giác ABC.
Advertisements (Quảng cáo)
(hình trang 122, 123 sgbt)

Trường hợp góc B nhọn :
Xét ∆ AMB và ∆ AND, ta có:
\(\widehat {AMB} = \widehat {AND} = 90^\circ \)
\(\widehat B = \widehat D\) (tính chất hình bình hành)
Suy ra: ∆ AMB đồng dạng ∆ AND (g.g)
Suy ra:
\(\eqalign{ & {{AM} \over {AN}} = {{AB} \over {AD}} \cr & \Rightarrow {{AM} \over {AB}} = {{AN} \over {AD}} \cr} \)
Mà AD = BC (tính chất hình bình hành)
Suy ra: \({{AM} \over {AB}} = {{AN} \over {BC}}\)
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay góc NAB = 90°
Suy ra: \(\widehat {NAM} + \widehat {MAB} = 90^\circ \) (1)
Trong tam giác vuông AMB ta có: \(\widehat {ABM} = 90^\circ \)
Suy ra: \(\widehat {MAB} + \widehat B = 90^\circ \) (2)
Từ (1) và (2) suy ra : \(\widehat {NAM} = \widehat B\)
Xét ∆ ABC và ∆ MAN, ta có:
\({{AM} \over {AB}} = {{AN} \over {BC}}\) (chứng minh trên )
(chứng minh trên )
Vậy ∆ ABC đồng dạng ∆ MAN (c.g.c)
Trường hợp góc B tù:
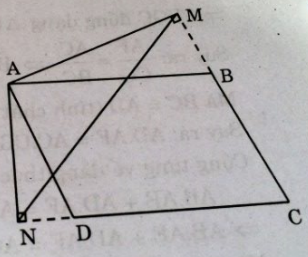
Xét ∆ AMB và ∆ AND, ta có:
\(\widehat {AMB} = \widehat {AND} = 90^\circ \)
\(\widehat {ABM} = \widehat {ADN}\) (vì cùng bằng góc C)
Suy ra: ∆ AMB đồng dạng ∆ AND (g.g)
Suy ra: \({{AM} \over {AN}} = {{AB} \over {AD}} \Rightarrow {{AM} \over {AB}} = {{AN} \over {AD}}\)
Mà AD = BC (tính chất hình bình hành )
Suy ra: \({{AM} \over {AB}} = {{AN} \over {BC}}\)
Vì AB // CD nên \(\widehat {ABC} + \widehat C = 180^\circ \) (3)
Tứ giác AMCN có \(\widehat {AMC} = \widehat {AND} = 90^\circ \)
Suy ra: \(\widehat {MAN} + \widehat C = 180^\circ \) (4)
Từ (3) và (4) suy ra : \(\widehat {MAN} = \widehat {ABC}\)
Xét ∆ AMN và ∆ ABC, ta có:
\({{AM} \over {AB}} = {{AN} \over {BC}}\) (chứng minh trên )
\(\widehat {MAN} = \widehat {ABC}\) (chứng minh trên )
Vậy ∆ MAN đồng dạng ∆ ABC (c.g.c)

