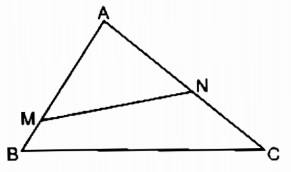
Câu 35: Cho tam giác ABC có AB = 12cm, AC = 15cm, BC = 18cm. Trên cạnh AB, đặt đoạn thẳng AM = 10cm, trên cạnh AC đặt đoạn thẳng AN = 8cm. Tính độ dài đoạn thẳng MN.
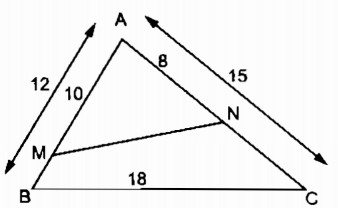
Ta có: \({{AM} \over {AC}} = {{10} \over {15}} = {2 \over 3}\)
\({{AN} \over {AB}} = {8 \over {12}} = {2 \over 3}\)
Suy ra: \({{AM} \over {AC}} = {{AN} \over {AB}}\)
Xét ∆ ABC và ∆ AMN, ta có:
\(\widehat A\) chung
\({{AM} \over {AC}} = {{AN} \over {AB}}\)
Suy ra: ∆ AMN đồng dạng ∆ ABC (c.g.c) \( \Rightarrow {{AN} \over {AB}} = {{MN} \over {BC}}\)
Vậy MN = \({{AN.BC} \over {AB}} = {{8.18} \over {12}} = 12\) (cm).
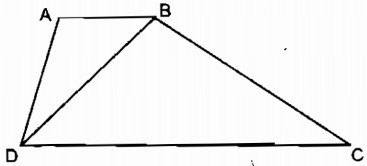
Câu 36: Hình thang ABCD (AB // CD) có AB = 4cm, CD = 16cm và BD = 8cm . Chứng minh \(\widehat {BAD} = \widehat {DBC}\) và BC = 2 AD.
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{ & {{AB} \over {BD}} = {4 \over 8} = {1 \over 2} \cr & {{BD} \over {DC}} = {8 \over {16}} = {1 \over 2} \cr} \)
Suy ra: \({{AB} \over {BD}} = {{BD} \over {DC}} = {1 \over 2}\)
Xét ∆ ABD và ∆ BDC, ta có:
\(\widehat {ABD} = \widehat {BDC}\) (so le trong)
\({{AB} \over {BD}} = {{BD} \over {DC}}\) (chứng minh trên )
Vậy ∆ ABD đồng dạng ∆ BDC (c.g.c) \( \Rightarrow \widehat {BAD} = \widehat {DBC}\)
Advertisements (Quảng cáo)
Tỉ số đồng dạng k \( = {1 \over 2}\)
Ta có: \({{AC} \over {BC}} = {1 \over 2}\), suy ra : BC = 2AD.
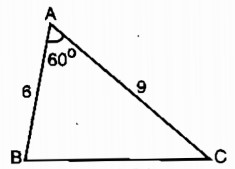
Câu 37: Cho tam giác ABC có \(\widehat A = 60^\circ \) , AB = 6cm, AC = 9cm
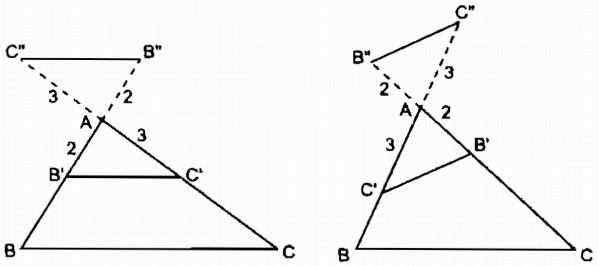
a. Dựng tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng k = \({1 \over 3}\)
b. Hãy nêu một vài cách dựng khác và vẽ hình trong từng trường hợp cụ thể.
Cách dựng:
– Trên cạnh AB dựng điểm B’ sao cho AB’ = 2cm.
– Trên cạnh AC dựng điểm C’ sao cho AC’ = 3cm.
– Nối B’C’.
Khi đó AB’C’ là tam giác cần dựng.
Chứng minh:
Theo cách dựng, ta có:
\({{AB’} \over {AB}} = {2 \over 6} = {1 \over 3}\)
\({{AC’} \over {AC}} = {3 \over 9} = {1 \over 3}\)
Suy ra: \({{AB’} \over {AB}} = {{AC’} \over {AC}}\)
Lại có: \(\widehat A\) chung
Vậy ∆ AB’C’ đồng dạng ∆ ABC (c.g.c)
b. Hình vẽ minh họa như sau: