Câu 32: Tam giác ABC có ba góc nhọn và có trực tâm là điểm H. Gọi K, M, N thứ tự là trung điểm của các đoạn thẳng AH, BH, CH.
Chứng minh rằng tam giác KMN đồng dạng với tam giác ABC với tỉ số đồng dạng k = \({1 \over 2}\) .
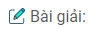
Trong tam giác AHB, ta có:
K là trung điểm của AH (gt)
M là trung điểm của BH (gt)
Suy ra KM là đường trung bình của tam giác AHB.
Suy ra: KM \( = {1 \over 2}AB\)
(tính chất đường trung bình của tam giác )
Suy ra: \({{KM} \over {AB}} = {1 \over 2}\) (1)
Trong tam giác AHC, ta có:
K là trung điểm của AH (gt)
N là trung điểm của CH (gt)
Suy ra KN là đường trung bình của tam giác AHC.
Suy ra: KN \( = {1 \over 2}AC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{KN} \over {AC}} = {1 \over 2}\) (2)
Trong tam giác BHC, ta có:
M trung điểm của BH (gt)
N trung điểm của CH (gt)
Suy ra MN là đường trung bình của tam giác BHC.
Advertisements (Quảng cáo)
Suy ra: MN \( = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{MN} \over {BC}} = {1 \over 2}\) (3)
Từ (1), (2) và (3) suy ra: \({{KM} \over {AB}} = {{KN} \over {AC}} = {{MN} \over {BC}} = {1 \over 2}\)
Vậy ∆ KMN đồng dạng ∆ ABC (c.c.c)
Ta có hệ số tỉ lệ: k \( = {{KM} \over {AB}} = {1 \over 2}\).
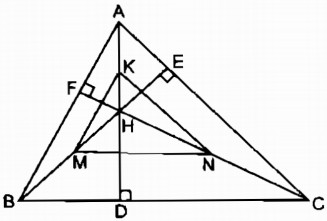
Câu 33: Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
b. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543cm.
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Advertisements (Quảng cáo)
Suy ra: \(PQ = {1 \over 2}AB\)
(tính chất đường trung bình của tam giác )
Suy ra: \({{PQ} \over {AB}} = {1 \over 2}\) (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: \(PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{PR} \over {AC}} = {1 \over 2}\) (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: \(QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{QR} \over {BC}} = {1 \over 2}\) (3)
Từ (1), (2) và (3) suy ra: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {1 \over 2}\)
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {{PQ + PR + QR} \over {AB + AC + BC}} = {{p’} \over p}\)
Vậy: \({{p’} \over p} = {1 \over 2} \Rightarrow p’ = {1 \over 2}p = {1 \over 2}.543 = 271,5\) (cm)
Câu 34: Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k \( = {2 \over 3}\)
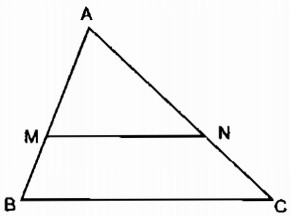
Cách dựng:
– Trên cạnh AB dựng điểm M sao cho AM = \({2 \over 3}\)AB
– Trên cạnh AC dựng điểm N sao cho AN = \({2 \over 3}\)AC
– Dựng đoạn thẳng MN ta được tam giác AMN đồng dạng với tam giác ABC theo tỉ số đồng dạng k = \({2 \over 3}\).
Chứng minh:
Theo cách dựng ta có:
\(\eqalign{ & AM = {2 \over 3}AB \Rightarrow {{AM} \over {AB}} = {2 \over 3} \cr & AN = AC \Rightarrow {{AN} \over {AC}} = {2 \over 3} \cr} \)
Suy ra: \({{AM} \over {AB}} = {{AN} \over {AC}}\)
Theo định lí đảo của định lí Ta-lét ta có: MN // BC
Vậy ∆ AMN đồng dạng ∆ ABC và k \( = {{AM} \over {AB}} = {2 \over 3}\).

