Câu 24: Tam giác vuông ABC có$\widehat A = 90^\circ $, AB = a (cm), AC = b (cm), (a < b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC) (h.20).
a. Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b. Hãy tính các đoạn thẳng trên đây chính xác đến chữ số thập phân thứ hai khi biết a = 4,15cm, b = 7,25cm.
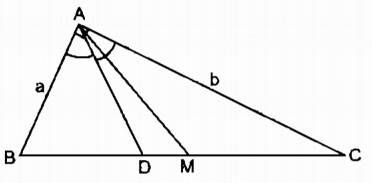
a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {a^2} + {b^2}\)
Suy ra: \(BC = \sqrt {{a^2} + {b^2}} \)
Ta có: AM = BM \( = {1 \over 2}BC\) ( tính chất tam giác vuông )
Suy ra: \(AM = {1 \over 2}\sqrt {{a^2} + {b^2}} \)
Vì AD là đường phân giác của \(\widehat {BAC}\) nên:
\({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác )
Suy ra: \({{DB} \over {DB + DC}} = {{AB} \over {AB + AC}}\)
hay \({{DB} \over {BC}} = {{AB} \over {AB + AC}}\)
Vậy: \(DC = BC – DB = \sqrt {{a^2} + {b^2}} – {{a\sqrt {{a^2} + {b^2}} } \over {a + b}} = {{b\sqrt {{a^2} + {b^2}} } \over {a + b}}\)
\(\eqalign{ & DM = BM – BD \cr & = {1 \over 2}\sqrt {{a^2} + {b^2}} – {{a\sqrt {{a^2} + {b^2}} } \over {a + b}} \cr & = {{b\sqrt {{a^2} + {b^2}} – a\sqrt {{a^2} + {b^2}} } \over {a + b}} \cr & = {{\left( {b – a} \right)\sqrt {{a^2} + {b^2}} } \over {a + b}} \cr} \)
Advertisements (Quảng cáo)
b. Với a = 4,15cm; b= 7,25 cm, sử dụng máy tính, ta tính được:
\(\eqalign{ & BC = \sqrt {{{\left( {4,15} \right)}^2} + {{\left( {7,25} \right)}^2}} \approx 8,35(cm) \cr & BD = {{4,15\sqrt {{{\left( {4,15} \right)}^2} + {{\left( {7,25} \right)}^2}} } \over {4,15 + 7,25}} \approx 3.04(cm) \cr & DC \approx 5,31(cm) \cr & AM \approx 4,18(cm) \cr & DM \approx 1,14(cm) \cr} \)
Câu 3.1: Tam giác ABC vuông tại A có đường phân giác AD. Biết rằng độ dài của các cạnh góc vuông AB = 3,75cm, AC = 4,5cm
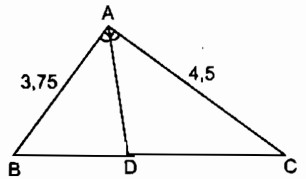
Hãy chọn kết quả đúng (tính chính xác đến chữ số thập phân).
1. Độ dài của đoạn thẳng BD là:
A. 18,58
B. 2,66
C. 2,65
D. 3,25
Advertisements (Quảng cáo)
2. Độ dài đoạn thẳng CD là:
A. 27,13
B. 2,68
C. 3,2
D. 3,15
1. Chọn B
2. Chọn C
Câu 3.2: Hình bình hành ABCD có độ dài cạnh AB = a = 12,5cm, BC = b = 7,25cm. Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F.
Hãy tính độ dài đường chéo AC, biết EF = m = 3,45cm.
(Tính chính xác đến hai chữ số thập phân)
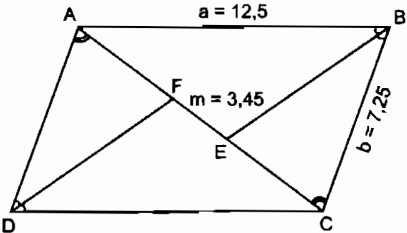
Vì ABCD là hình bình hành nên\(\widehat {ABC} = \widehat {ADC}\). Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra \(\widehat {ADF} = \widehat {CBE}\)
Mặt khác, ta có: AD = CB = b;
\(\widehat {DAF} = \widehat {BCE}\) (so le trong)
Suy ra: ∆ ADF = ∆ CBE (g.c.g)
⇒ AF = CE
Đặt AF = CE = x
Theo tính chất của đường phân giác BE trong tam giác ABC, ta có:
\(\eqalign{ & {{AB} \over {BC}} = {{AE} \over {CE}} = {{AF + FE} \over {CE}} \cr & \Rightarrow {a \over b} = {{x + m} \over x} \Rightarrow x = {{mb} \over {a – b}} \cr & AC = 2x + m = {{2mb} \over {a – b}} + m = {{m\left( {a + b} \right)} \over {a – b}} \cr} \)
Thay số, tính trên máy tính điện tử cầm tay ta được:
\(AC = {{3,45\left( {12,5 + 7,25} \right)} \over {12,5 – 7,25}} \approx 12,98\) (cm)

