Câu 28: Hình thang ABCD (AB // CD) có CD = 2AB. Gọi E là trung điểm của DC. Chứng minh rằng ba tam giác ADE, ABE và BEC đông dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau).
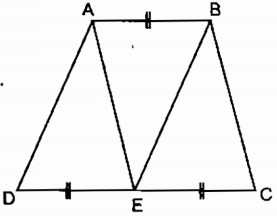
Vì CD = 2AB (gt) nên AB \( = {1 \over 2}CD\)
Vì E là trung điểm của CD nên DE = EC \( = {1 \over 2}CD\)
Suy ra: AB = DE = EC
Hình thang ABCD có đáy AB = EC nên hai cạnh bên AE và BC song song với nhau:
Xét ∆ AEB và ∆ CBE, ta có:
\(\widehat {ABE} = \widehat {BEC}\) (so le trong)
\(\widehat {AEB} = \widehat {EBC}\) (so le trong)
Advertisements (Quảng cáo)
BE canh chung
⇒ ∆ AEB = ∆ CBE (g.c.g) (1)
Hình thang ABED có đáy AB = DE nên hai cạnh bên AD và BE song song với nhau.
Xét ∆ AEB và ∆ EAD, ta có:
\(\widehat {BAE} = \widehat {AED}\) (so le trong)
Advertisements (Quảng cáo)
\(\widehat {AEB} = \widehat {EAD}\) (so le trong)
AE cạnh chung
⇒ ∆ AEB = ∆ EAD (g.c.g) (2)
Từ (1) và (2) suy ra: ∆ AEB = ∆ EAD = ∆ CBE.
Câu 4.1: Tam giác ABC có tổng độ dài hai cạnh AB + AC = 10,75 cm và đồng dạng với tam giác A’B’C’ có độ dài các cạnh A’B’ = 8,5cm, A’C’ = 7,35cm, B’C’ = 6,25cm.
Tính chính xác đến hai chữ số thập phân, chu vi của tam giác ABC là:
A. 45,36
B. 14,46
C. 14,98
D. 14,50
Hãy chọn kết quả đúng
Chọn C
